2-List Stable Matching: The Easiest Problem I Couldn't Solve in My PhD

I thought it'd be fun to write two complementary posts: "The hardest problem I solved in my PhD" (WIP) and "The easiest problem I couldn't solve in my PhD" (this one).
I'll state the problem, why I think it's easy despite not solving it, and talk a bit about what I tried.
With GPT-5, the claim is that reasoning LLMs can handle "PhD-research-level problems", so I'd like to submit this problem as a candidate. If anyone has GPT Pro, I'd love to see what it comes up with for this problem!
Problem Statement: 2-List Stable Matching
The 2-list stable matching problem is the special case of the classic stable matching problem where, instead of each individual having their own preference list, there are only two different preference lists that each side can pick from.
Setting: Even though stable matching has serious applications in market design, we'll explain it in the traditional setting of matching n straight men and n straight women for marriage.
We identify the men with numbers from 0 to n-1, and the same for the women.
We have to pair them up based on only two factors, which we will call X and Y.
To make it concrete (and leaning into the silly marriage setting), we could think of X as IQ and Y as net worth; however, X and Y could be any attributes that we can objectively rank the people by.
In this simplified setting, each person only cares about one of the two factors: they either rank the other side by X, or they rank them by Y.
Input: We are given six things:
men_x_ranking: A list of the men ordered byX.men_y_ranking: A list of the men ordered byY.women_x_ranking: A list of the women ordered byX.women_y_ranking: A list of the women ordered byY.men_preferences: A list indicating whether each man cares aboutXorY.women_preferences: A list indicating whether each woman cares aboutXorY.
Constraints:
- All the lists have length
n. - The first four lists contain the numbers from
0ton-1in some order. For instance,men_x_ranking = [0, 1, 2]means that man0is the best in terms ofX, man1is the second best, and man2is the last. - The last two lists only contain characters
'X'and'Y'. For instance, ifmen_preferences = ['Y', 'X', 'Y'], it means that men0and2rank the women by'Y', and man1ranks the women by'X'.
Example input:
men_x_ranking = [0, 1, 2]
men_y_ranking = [1, 0, 2]
women_x_ranking = [2, 1, 0]
women_y_ranking = [2, 0, 1]
men_preferences = ['Y', 'X', 'Y']
women_preferences = ['X', 'X', 'X']
Another way to think about the input is to look at the ranking for each person:
M0: W2, W0, W1
M1: W2, W1, W0
M2: W2, W0, W1
W0: M0, M1, M2
W1: M0, M1, M2
W2: M0, M1, M2
The input format above is equivalent but more compact, given that there are at most two unique preference rankings among all men (and the same for the women). Listing all the preferences takes O(n^2) space, while the compact format only takes O(6*n) = O(n) space.
Output format: We have to return a list of n pairs, indicating who is going to marry whom as (man, woman) pairs. All men and women must appear exactly once.
Example output:
[(0, 2), (1, 1), (2, 0)]
Goal: Not all matchings are valid outputs. We must return a stable matching, which is a matching where there are no blocking pairs.
A blocking pair is a man-woman pair that (a) are not matched to each other, and (b) both prefer each other over their assigned partners.
The reason we don't want blocking pairs is that the man and woman in the blocking pair would be incentivized to "break" the arrangement and marry each other instead. In contrast, if there is no blocking pair, some people won't get their top choice--maybe even their last--but what matters is that they are not reciprocated by someone who also prefers them back. So, just because a matching is stable, it does not mean that everyone is happy.
For example, to check if the matching M0-W2, M1-W1, M2-W0 is stable, we can look at every unmatched couple and check if they form a blocking pair:
| Couple | Matched | Would the
| Would the
| Blocking pair |
|---|---|---|---|---|
| M0 and W0 | No | No | YES | No |
| M0 and W1 | No | No | YES | No |
| M0 and W2 | Yes | N/A | N/A | No |
| M1 and W0 | No | No | YES | No |
| M1 and W1 | Yes | N/A | N/A | No |
| M1 and W2 | No | YES | No | No |
| M2 and W0 | Yes | N/A | N/A | No |
| M2 and W1 | No | No | No | No |
| M2 and W2 | No | YES | No | No |
Since there are no blocking pairs, the matching is stable.
In contrast, to show that a matching is not stable, it suffices to find a single blocking pair.
For instance, for the same input, M0-W2, M1-W0, M2-W1 is not stable because M1 prefers W1 over W0 and W1 prefers M1 over M2.
What I was trying to do during my PhD was:
Solve the 2-list stable matching problem in less than O(n^2) time, or prove that O(n^2) is optimal.
This was a problem posed in the 2016 paper "Subquadratic Algorithms for Succinct Stable Matching" by Marvin Künnemann, Daniel Moeller, Ramamohan Paturi, Stefan Schneider.
Background: Stable Matching
As mentioned, the 2-list stable matching problem is a special case of the stable matching problem, also known as the stable marriage problem. The goal is the same, to find a stable matching, but the difference is that each single man and woman has their own subjective preference list.
Here is what is known about the original setting:
- The input size is
O(n^2). - A stable matching always exists.
- The Gale-Shapley algorithm finds a stable matching in
O(n^2)time. - In the worst case, we may need to examine
Θ(n^2)entries in the preference lists, so Gale-Shapley is runtime-optimal. (Source)
I won't explain the algorithm in detail, but here is a cute Numberphile video on it.
The algorithm involves a series of rounds, where everyone starts single. At each round, the remaining single men propose to their highest-ranked woman who has not rejected them yet. If the woman is not already engaged, she accepts the proposal. If she is, she can accept or reject it, depending on who she prefers. If she accepts, then her previous match goes back to the single pool.
Even though it is not obvious, it can be shown that after at most n rounds, everyone will be matched, and the matching will be stable.
Why Subquadratic Time Feels Plausible
Since the 2-list version is a special case, it is also true that a stable matching always exists, and we can use the Gale-Shapley algorithm to find one in O(n^2) time.
The question, then, is whether we can do better than Gale-Shapley in the 2-list case.
Here are two reasons why it "feels like" subquadratic should be possible:
Reason 1: The input size for the 2-list case is only O(n), while in the general case it is O(n^2).
The proof that Gale-Shapley is runtime-optimal uses the fact that we may need to examine Θ(n^2) entries in the preference lists, which obviously does not apply to the 2-list case.
Reason 2: If we consider the next special case, the 1-list version, the problem becomes trivial.
If all the men share the same preference list, and all the women share the same preference list, we can just match the most "popular" couple and repeat with the remaining people. This takes O(n) time.
So, the best we can do is Θ(n) time for the 1-list case and Θ(n^2) time for the n-list case (the general case). There must be some threshold k, with 1 < k < n, where the best we can do for the k-list case reaches Θ(n^2) time. The question is, what is k? Is it 2?
My conjecture is that k > 2. Even the (n, 1)-list case, where one side has arbitrary preferences and the other side all share the same list, can be solved in O(n) time with a similar greedy approach as the 1-list case.1
Geometric Interpretation
My advisor suggested a geometric interpretation: we can plot the people on a plane, where the x-axis corresponds to their rank for the X attribute and the y-axis corresponds to their rank for the Y attribute. Then, each person ranks the other set either by their x-coordinate or by their y-coordinate. This is an equivalent formulation of the problem.
Here is an example with 10 men and 10 women:
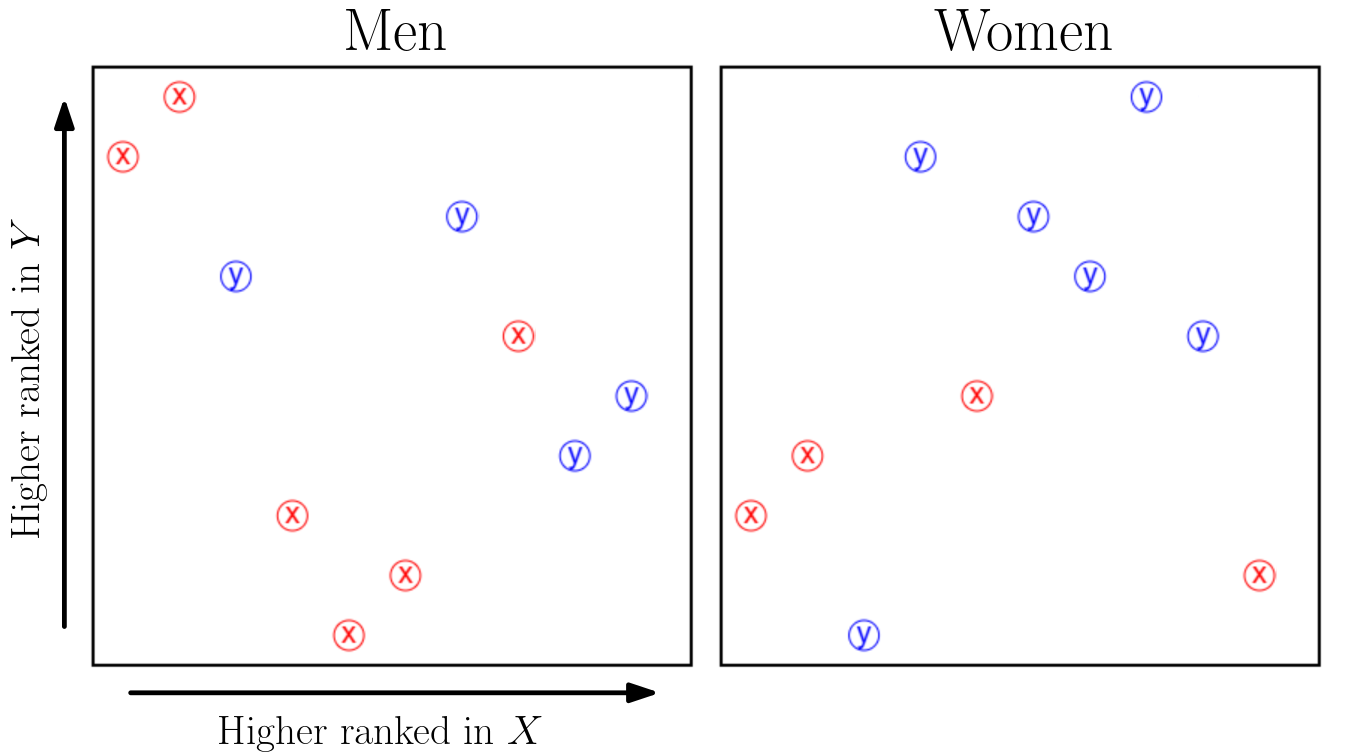
The left plane shows the men, while the right one shows the women.
Each person is labeled with a red X if they care about the X attribute, or a blue Y if they care about the Y attribute.
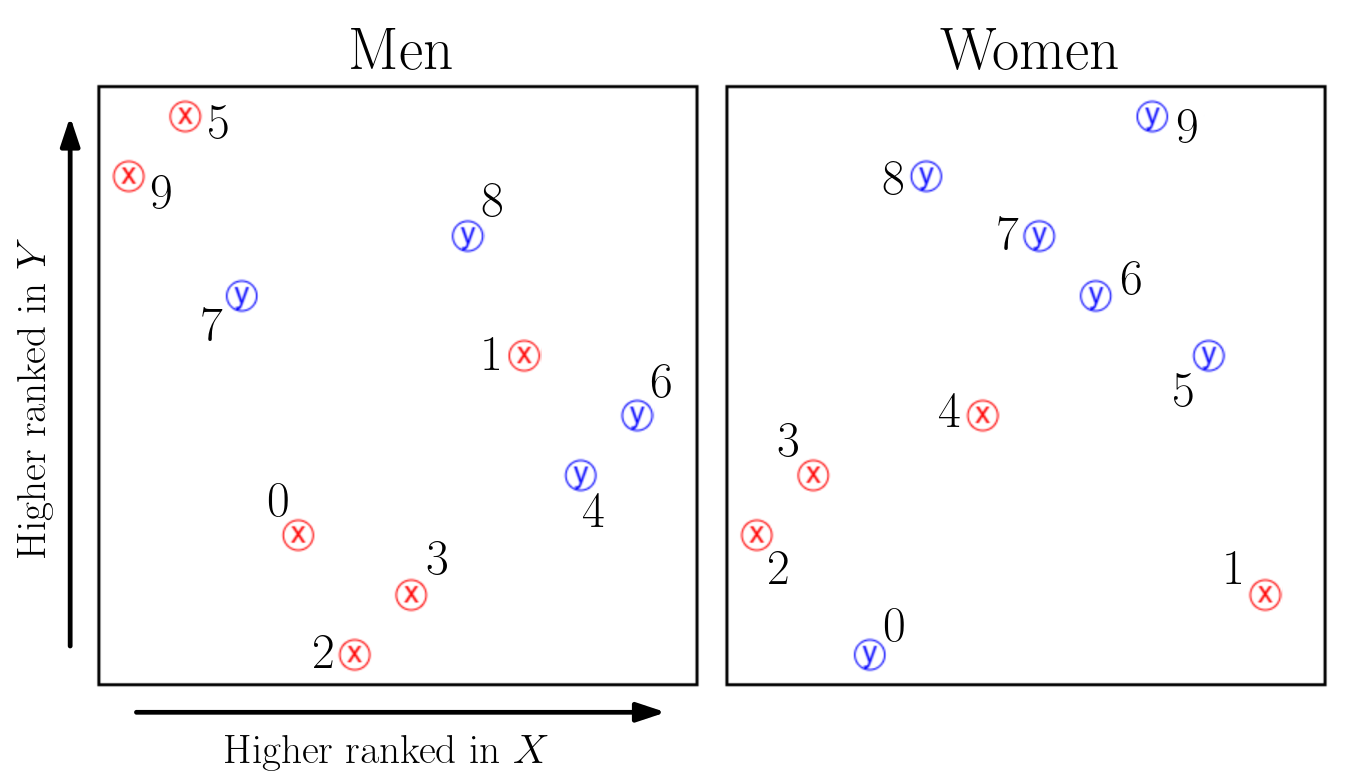
Here is a sample stable matching:
The geometric interpretation allows us to think geometrically. For instance, if we are to find a greedy strategy, it makes sense to focus on maximal points: points with the highest X or Y rank. In the image below, we labeled the maximal X-preferring men, Y-preferring men, X-preferring women, and Y-preferring women with parentheses.
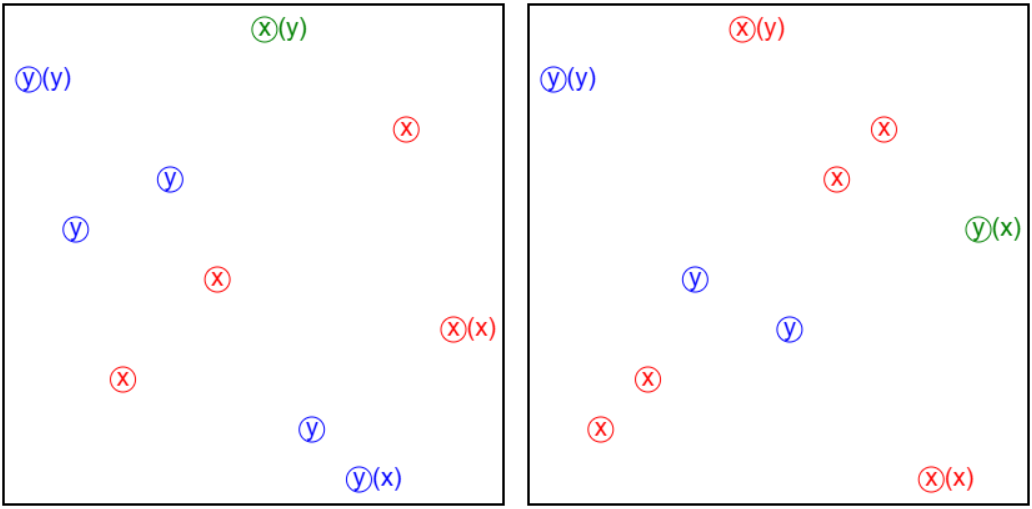
There are up to 8 maximal points. Sometimes, among the maximal points, we may find "soulmates": pairs of points that have each other as their top choice. In the image above, the green points are the top-Y man and the top-X woman, and they are soulmates.
Soulmates must be matched to each other. Otherwise, they'd form a blocking pair. In easy cases, we can find soulmates, match them, and repeat until everyone is matched. The hard case is when there are no soulmates.
However, sometimes the maximal points form a cycle such that no soulmates exist. Then, it's not clear how to proceed with a greedy algorithm. Love triangles can be a headache.
The images above come from an interactive demo I created to explore the problem space. It allows you to move the points around and see how that affects the stable matching. E.g., try dragging a point to the top-right corner, which makes them the top choice of everyone on the other side.
I think this demo should be useful for anyone looking to tackle the problem.
Final Thoughts
I lost my notes on the problem, so I can't recall everything I tried, but I think it's the problem that has gnawed at me the most from my research.2 Anyway; reasoning‑mode LLMs, here's your chance!
I once gave a lecture on stable matching, and I had two groups of four students volunteer to simulate the rounds of the algorithm. The idea was that they'd make their own rankings and, even though I had no control over their preferences, at the end, they'd all be matched and the matching would be stable.
Since matching undergrads for marriage would not be appropriate, I had them roleplay as med students and hospitals (residency matching is a real application of stable matching), with cardboard cutouts and everything.

Want to leave a comment? You can post under the linkedin post or the X post.
Footnotes
-
If all the men agree on the same list, we can go to their top choice
Wiand match her with her top choice,Mj. Otherwise,MjandWiwould form a blocking pair. We can then remove them, and repeat with the remaining people. ↩ -
I recently solved a problem that gnawed at me even more, the double-edge cut problem. I hope this one falls next! ↩