Building Lego castles with recurrences, memoization, and math

We'll walk through four solutions to an original coding problem, starting with a O(n^2) time and O(n) space solution, and progressively improving it with various techniques. This is one of my favorite problems to use as an interviewer, as there are many ways to go about it!

Statement

You want to build an n-story 2D Lego castle following these instructions:

• A 1-story castle is just a 1x1 block.
• An n-story castle is made with two (n-1)-story castles, side by side, one unit apart, with a row of blocks above them connecting them.

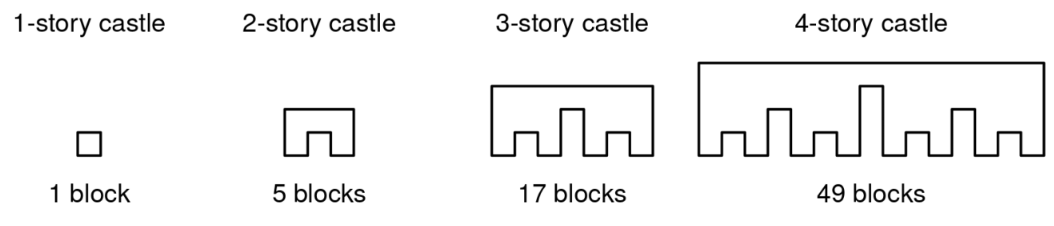
Given n > 0, how many 1x1 blocks will you need to buy to build an n-story castle?

Examples:

1-story castle: 1 block
2-story castle: 5 blocks
3-story castle: 17 blocks
4-story castle: 49 blocks
5-story castle: 129 blocks

Constraints:

• Assume that the solution will fit in a signed 64-bit integer.

Solution

Recurrence relation

A recurrence relation is a formula defined in terms of itself with smaller inputs. Since Lego castles are defined in terms of smaller castles, this problem is a good candidate for a recurrence relation.

We're trying to find a formula, blocks(n), which returns the number of blocks needed for an n-story castle. We know that:

• blocks(1) = 1
• for n > 1, blocks(n) can be obtained from blocks(n - 1) somehow.

We can break down the problem by introducing another function, roof(n), representing the number of blocks in the top row of an n-story castle. This makes the recurrence relation for blocks(n) straightforward:

blocks(n) = 2 * blocks(n - 1) + roof(n)

Next, we need to tackle roof(n). We can again use a recurrence relation:

• roof(1) = 1
• for n > 1, roof(n) = 2 * roof(n - 1) + 1

We can turn this recurrence relation into recursive code:

def roof(i):
  if i == 1:
    return 1
  return roof(i - 1) * 2 + 1

def blocks(n):
  if n == 1:
    return 1
  return blocks(n - 1) * 2 + roof(n)

Analysis:

• Time: O(n^2) - due to the repeated computations of roof(i) for each i.
• Space: O(n) - for the call stack.

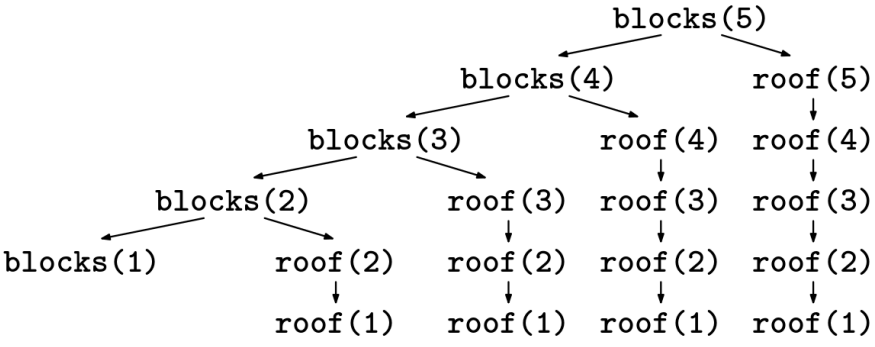
Here is the call tree for blocks(5) for the recursive implementation above:

Memoization

To optimize the solution, we can use memoization to avoid recomputing the same values of roof(n) multiple times. The idea of memoization is that, whenever we compute a value, roof(i), we store it in a map. Next time we need it, we can just look it up in the map instead of recomputing it.

Here is the implementation:

def blocks_memoized(n):
  memo = dict()

  def roof(n):
    if n == 1:
      return 1
    if n in memo:
      return memo[n]
    memo[n] = roof(n - 1) * 2 + 1
    return memo[n]

  def blocks_rec(n):
    if n == 1:
      return 1
    return blocks_rec(n - 1) * 2 + roof(n)

  return blocks_rec(n)

Analysis:

• Time: O(n) - with memoization, each value of roof(i) is computed exactly once.
• Extra space: O(n) - for the memoization table and the call stack.

Bottom-up approach

If we look at the first few values of roof(n), they are:

1, 3, 7, 15, ...

We can reverse engineer the pattern: they are powers of 2 minus 1. We can give a closed formula:

roof(n) = 2^n - 1

This simplifies our code, as we don't need memoization anymore.

To get down to O(1) extra space, we also need to stop using recursion, as a call stack of depth n takes O(n) space. We can move from the recursive implementation to a bottom-up, iterative implementation:

def blocks_iterative(n):
  blocks = 1
  for i in range(2, n + 1):
    roof = 2**i - 1
    blocks = blocks * 2 + roof
  return blocks

Analysis:

• Time: O(n)
• Extra space: O(1)

Closed formula approach

In an interview, the memoized recursive solution is probably what the interviewer is looking for. However, there is also a closed formula for this problem, which allows us to compute the number of blocks in an n-story castle in constant time.

We'll think of the total number of blocks as a sum of all the individual roofs:

blocks(n) = roof(n) + 2 * roof(n - 1) + 4 * roof(n - 2) + ... + 2^(n-1) * roof(1)

To simplify further, it will help to put this in summation notation. In math, we would use the Sigma symbol, ∑. In an interview, we can simply type it like this:

blocks(n) = SUM FROM k = 0 TO n-1 OF 2^k * roof(n - k)

Using the formula for roof(n - k), we get:

blocks(n) = SUM FROM k = 0 TO n-1 OF 2^k * (2^(n-k) - 1)

We can simplify the expression inside the sum:

2^k * (2^(n-k) - 1) = 2^k * 2^(n-k) - 2^k = 2^n - 2^k

Now that the term inside the sum is split into two parts, we can separate them into two sums:

blocks(n) = (SUM FROM k = 0 TO n-1 OF 2^n) - (SUM FROM k = 0 TO n-1 OF 2^k)

Finally, we can simplify each sum individually.

The first one is just adding 2^n a total of n times, so it is n * 2^n.

The second one is a 1 + 2 + 4 + ... + 2^(n-1), a classic geometric series. When dealing with powers of two, it is often handy to know that the sum of the first few powers of 2 always falls one short of the next power of 2:

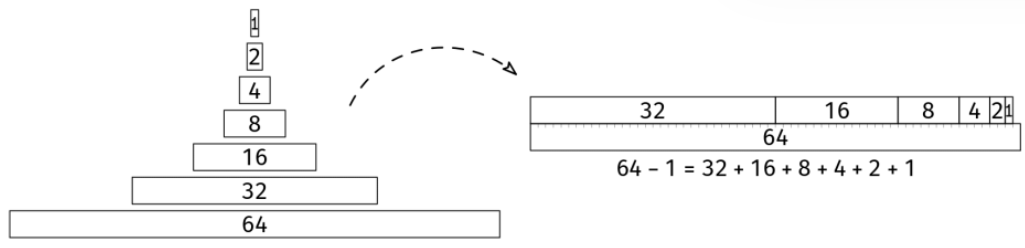
Thus, the second sum is just 2^n - 1.

Bringing it all together, we get:

blocks(n) = n * 2^n - (2^n - 1)

Here is the implementation:

def blocks_math(n):
  return n * 2**n - (2**n - 1)

Analysis:

• Time: O(1)
• Extra space: O(1)

Caveat about large numbers

Even though the math approach does not have any loops, note that the value of the answer grows exponentially, so the number of bits in the answer does grow linearly with n. In that sense, the math approach takes O(n) time just to write the output (and the other approaches take even more). The constant time analysis is only valid for small values of n, where we can handle all operations with 64-bit integers, or under the simplifying assumption that math operations always take constant time regardless of how large the numbers are.

For this problem, the solutions fit in signed 64-bit integers up to n = 57.

On a related note, recall that Python has arbitrary precission integers, so we won't get overflow errors even for large values of n.

Follow-up question: 3D Lego castle

This time, you want to build an n-story 3D Lego castle following these instructions:

• A 1-story castle is just a 1x1x1 block.
• An n-story castle is made of four (n-1)-story castles, placed in a square with adjacent castles one unit apart, and with a layer of blocks above them connecting them.

This image shows the 1-story, 2-story, and 3-story castles:

Given n > 0, how many 1x1x1 blocks will you need to buy to build an n-story castle?

Examples:

1-story castle: 1 block
2-story castle: 13 blocks
3-story castle: 101 blocks
4-story castle: 629 blocks

Constraints:

• Assume that the solution will fit in a signed 64-bit integer.

Solution to the follow-up

For this variation, I came up with this new recurrence relation:

3d_blocks(n) = 4 * 3d_blocks(n - 1) + roof_side(n)^2

where roof_side(n) is the number of blocks in the side of the roof of an n-story castle. In fact, roof_side(n) is exactly the same as roof(n) in the 2D case.

From here, we can turn the recurrence relation into recursive code and memoize it, or turn it into an iterative bottom-up solution, just like we did in the 2D case.

The only approach that requires some additional work is the closed formula approach.

Closed formula for the follow-up

Again, we'll think of the total number of blocks as a sum of all the individual roofs:

3d_blocks(n) =   1 * roof_side(n)^2
               + 4 * roof_side(n - 1)^2
               + 4^2 * roof_side(n - 2)^2
               + ...
               + 4^(n-1) * roof_side(1)^2

Expressed as a summation:

3d_blocks(n) = SUM FROM k = 0 TO n-1 OF 4^k * roof_side(n - k)^2

Using the formula for roof_side(n - k), we get:

3d_blocks(n) = SUM FROM k = 0 TO n-1 OF 4^k * (2^(n-k) - 1)^2

We can simplify the expression inside the sum:

4^k * (2^(n-k) - 1)^2 = 2^(2n) - 2^(n+k+1) + 2^(2k)

Now that the term inside the sum is split into three parts, we can separate them into three sums:

3d_blocks(n) = (SUM FROM k = 0 TO n-1 OF 2^(2n)) -
               (SUM FROM k = 0 TO n-1 OF 2^(n+k+1)) +
               (SUM FROM k = 0 TO n-1 OF 2^(2k))

We can now simplify each sum individually:

3d_blocks(n) = (n * 2^(2n)) -
               (2^(2n+1) - 2^(n+1)) +
               (((4^n)-1)/3)

We can now turn this into code.

Conclusions

I wanted to highlight this problem from the book because it ties together a few topics nicely. Thanks to Eugene Kovko and Ebadul Islam Farooqi for the idea of coming up with a closed formula solution -- it had completely escaped me when we wrote the book!

If you like this teaching style, check out the book on Amazon. See also my blog post with all the BCtCI free resources.

---

Want to leave a comment? You can post under the linkedin post or the X post.