Top-K Problems: Sorting vs Heaps vs Quickselect

One of the most classic problems in coding interviews is:

Top-K Problem: Given an array of n integers, and an integer k ≤ n, return the k smallest values.

We'll consider two variants: one in which we need to return the elements in sorted order, and the other in which we can return them in any order.

The following table summarizes the different approaches and runtimes:

|       Approach       |         Unsorted Output         |          Sorted Output          |
|                      |      Time      |      Space     |      Time      |      Space     |
| -------------------- | ------------------------------- | ------------------------------- |
| Sorting              | O(n log n)     | O(n)           | O(n log n)     | O(n)           |
| Min Heap             | O(n + k log n) | O(n)           | O(n + k log n) | O(n)           |
| Max Heap of size k   | O(n log k)     | O(k)           | O(n log k)     | O(k)           |
| Quickselect          | O(n)           | O(n)           | O(n + k log k) | O(n)           |
| ???                  | O(n)           | O(k)           | O(n + k log k) | O(k)           |

Assumptions:

• Even though the problem is worded in terms of integers, we want to support generic comparison logic for the elements, so the O(n log n) sorting lower bound applies. Otherwise, specialized integer sorting algorithms like radix sort could affect the analysis.
• If we modify the input array, we count that as using space.

We can see that:

• Quickselect is best to optimize runtime, while heaps are best to optimize space.
• The best possible time depends on whether the output needs to be sorted or not.
• As of now, I don't know of any algorithm that combines the runtime of Quickselect and the space complexity of the max-heap solution (the ??? row).

In this post, we'll explain the four approaches and show the Python implementations.

Instead of the k smallest values, we could also ask for the k largest values. The problem is essentially the same.

Sorting solution

This question is trivial if we sort the input. After sorting, we get the first k elements.

# O(n log n) time, O(n) space
def sorting_approach(arr, k):
    arr.sort()
    return arr[:k]  # Sorted output

Even if we sort the array in-place, keep in mind that most built-in sorting libraries use O(n) extra space internally.

Min-heap solution

Sorting is 'overkill' because, even if we need to sort the elements we return, we don't need to sort the rest.

A natural approach for problems involving partial sorts is to use a heap. We could dump the array into a min-heap and pop the k smallest numbers:

# O(n + k log n) time, O(n) space
def min_heap_approach(arr, k):
    heapq.heapify(arr)
    return [heapq.heappop(arr) for _ in range(k)]  # Sorted output

This approach leverages that we can build a heap in linear time with heapify. After that, we do k heap pops. Since the heap has O(n) elements, each pop takes O(log n) time.

To learn more about heaps, check out the Implement a Heap problem in the BCtCI online materials.

Max-heap solution

Alternatively, we could use max-heap and keep track of the smallest k elements as we iterate through them. We use a max-heap so that the largest element among the smallest k is always at the root, making it easy to remove it when we need to make space for a smaller element.

The algorithm is simple: for each element, we push it to the max-heap. If the heap size exceeds k, we pop the largest element (which is guaranteed to be at the root of the max-heap). This ensures that the heap always contains the k smallest elements seen so far.

# O(n log k) time, O(k) space
def max_heap_approach(arr, k):
    max_heap = []
    for num in arr:
        heapq.heappush(max_heap, -num)  # Negate values to simulate a max-heap
        if len(max_heap) > k:
            heapq.heappop(max_heap)
    return [-x for x in max_heap]  # Unsorted output

Since the heap size never exceeds k, each heap operation only takes O(log k) time. However, we don't benefit from heapify.

If we wanted a sorted output, we can pop the elements from the max-heap one by one instead of directly returning the underlying array of heap elements. This would add an extra O(k log k) factor to the runtime, but the O(n log k) still dominates.

This is the most space-efficient solution.

Quickselect solution

To get to the most efficient solution, we need to realize that we can use this property:

Property 1: We only need to find the kth smallest element. After that, we can do a single pass to get all the elements equal to or smaller than it.

So, how do we find the kth smallest element? This is the exact problem solved by the Quickselect algorithm.

For now, assume that we had a quickselect() function that returns the kth smallest element of an array. Here is how we would use it:

# O(n) time, O(n) space
def quickselect_approach(arr, k):
    kth_smallest = quickselect(arr, k)
    result = [x for x in arr if x < kth_smallest]
    while len(result) < k:
        result.append(kth_smallest)
    return result  # Unsorted output -- return sorted(result) for sorted output.

The while loop is necessary because of duplicates in the array. If we initialized res as the subset of arr that is less than or equal to kth_smallest, we may have ended with more than k elements if arr contains duplicates of kth_smallest. It's easier to first add all the elements less than kth_smallest, and then add as many copies of kth_smallest as needed to reach k elements.

As we'll see, quickselect() runs in O(n) time. If we don't need to sort the output, Quickselect is the bottleneck. If we need to output the k smallest elements sorted, the runtime becomes O(n + k log k).

Finally, let's show how to implement the quickselect() function.

Quickselect

Recall the Quicksort partition step:

# O(n) time, O(n) space
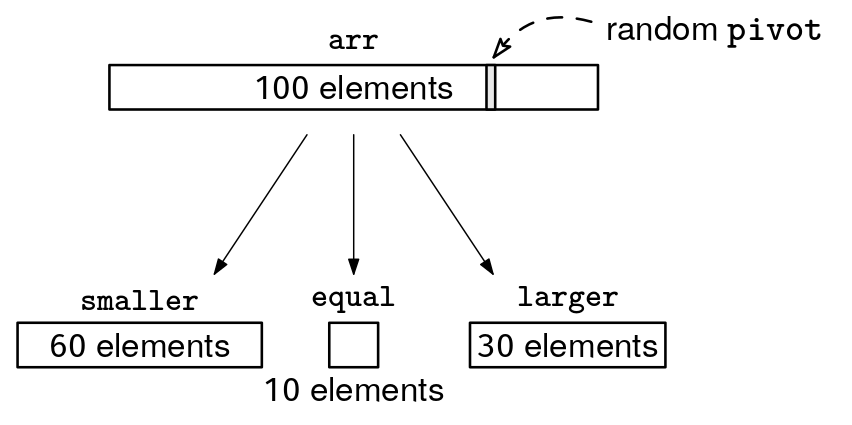
def partition(arr):
    pivot = random.choice(arr)
    smaller, equal, larger = [], [], []
    for x in arr:
        if x < pivot:
            smaller.append(x)
        elif x == pivot:
            equal.append(x)
        else:
            larger.append(x)
    return smaller, equal, larger

If the array can contain duplicates, equal may contain multiple elements:

The key is to think about the position of the pivot:

Property 2: After the quicksort partition step, we know exactly how many elements are smaller than the pivot. Thus, we can deduce the actual index of the pivot (or indices, if the pivot has duplicates) in the sorted order.

Let S and E represent the number of elements in the smaller and equal arrays, respectively. We can do a case analysis to see whether the kth smallest element is in smaller, equal, or larger:

1. Case 1: k <= S. The kth smallest element is in smaller.
2. Case 2: S < k <= S + E. The kth smallest element is in equal.
3. Case 3: k > S + E. The kth smallest element is in larger.

In Quickselect, we do this case analysis and act accordingly:

1. Case 1: We can recursively search for the kth smallest element in smaller.
2. Case 2: The pivot is the kth smallest element. We return it directly.
3. Case 3: We can recursively search for the (k - S - E)th smallest element in larger.

For example, if S = 60, E = 10, and L = 30, and k = 76, we would need to search for the 6th smallest element in larger.

The implementation is similar to quicksort. In particular, the partition logic is the same. The main difference is that we have a single recursion call depending on the case analysis, a bit like in binary search.

# O(n) time, O(n) space
def quickselect(arr, k):
    smaller, equal, larger = partition(arr)
    S, E = len(smaller), len(equal)

    if k <= S:
        return quickselect(smaller, k)
    elif k <= S + E:
        return equal[0]
    else:
        return quickselect(larger, k - S - E)

Here is a full example, where we are looking for the 5th smallest element. The 5th smallest element is highlighted in red.

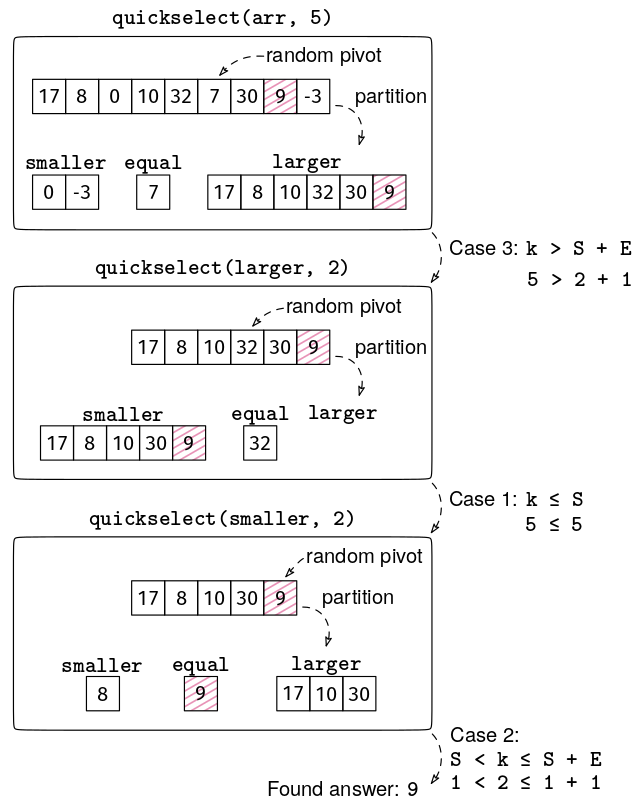
Quickselect is not common in interviews, but it's not hard to implement if you already understand quicksort, so you can add it to your bag of tricks.

Quickselect analysis

Quickselect runs in linear time with high probability, but the analysis is a bit tricky because it depends on how lucky we get with the pivots. To be clear, the analysis below is beyond what's expected for coding interviews.

The key question is: when we make a recursive call, how small is the new array (smaller or larger) relative to arr? How much is the array size reduced at each step?

As you probably know from the analysis of binary search, if the array is reduced by 50% at each step, the number of steps is log_2(n). (The definition of log_2(n) is "the number of times you can divide n by 2 until you get 1".)

However, we don't need the reduction to be 50% at each step. As long as the reduction is at least some constant fraction at each step (like, e.g., 25%), the number of steps is still logarithmic, just with a different base. In the end, it's still O(log n), since the base of logarithms goes away in big O notation.

The problem with Quickselect is that we don't always reduce the array by a constant fraction. For instance, if k is 1, and the random pivot happens to be the largest element, we'll only eliminate 1 element (the pivot itself). That's why, in the worst case with the worst possible luck, the number of steps is O(n).

However, since the pivot is random, there's a 50% chance that the pivot will be in the middle n/2 elements of arr. If that happens, at least 25% of the elements will be eliminated from the search range: if k is larger than the pivot's position, we'll eliminate the n/4 smallest elements, and if k is smaller than the pivot's position, we'll eliminate the n/4 largest elements.

Eliminating a constant fraction of the elements (at least 25%) with a 50% chance is enough to guarantee that the number of recursive calls is O(log n) with high probability. As n grows, the probability of being unlucky becomes negligible (approaches 0 exponentially fast).

The final recurrence for the expected worst-case runtime of Quickselect is:

T(n) = O(n) * s + T(0.75n)

Where:

• O(n) is the runtime of the partition step.
• s is the number of steps until the array gets reduced by at least 25%.
• T(0.75n) is the runtime of the remaining 75% of the array recursively.

As we discussed, there's a >50% chance that s is 1, so the expected value of s is O(1). This leaves:

T(n) = O(n) + T(0.75n) = O(n + 0.75n + (0.75)^2 n + ...)

The infinite geometric series 1 + 0.75 + (0.75)^2 + ... converges to 4, so we can simplify the whole thing to T(n) = O(4n) = O(n).

Quickselect variations

If we don't want to deal with expected runtimes, there's a method to pick good pivots deterministically, called Median of Medians. It guarantees a deterministic worst-case runtime of O(n). However, the random pivot is faster in practice and easier to implement (especially relevant in interviews).

There's also an in-place version of Quickselect. The version we showed takes O(n) expected extra space because we declare new smaller, equal, and larger arrays. If we are allowed to modify the input, there is an in-place version of Quickselect that rearranges the array in-place to put the smaller elements first, then the pivot(s), and then the larger elements. Then, the expected extra space would be O(log n), with the recursion stack as the bottleneck. With an iterative implementation, we can bring this further down to O(1).

Conclusion

This post shows one of the connections between sorting, heaps, and Quickselect. In interviews, whenever a problem involves sorting in some capacity, consider if one of these adjacent approaches can yield a better solution.

I'll end with a question:

Is it possible to achieve the runtime of Quickselect with the space complexity of the max-heap solution?

That is:

• Unsorted output variant: can it be solved in O(n) time and O(k) extra space without modifying the input?
• Sorted output variant: can it be solved in O(n + k log k) time and O(k) extra space without modifying the input?

The answer is probably already known, but I haven't looked into it. If you have any ideas, please let me know!

---

Want to leave a comment? You can post under the linkedin post or the X post.