Single-Edge Cut Problem
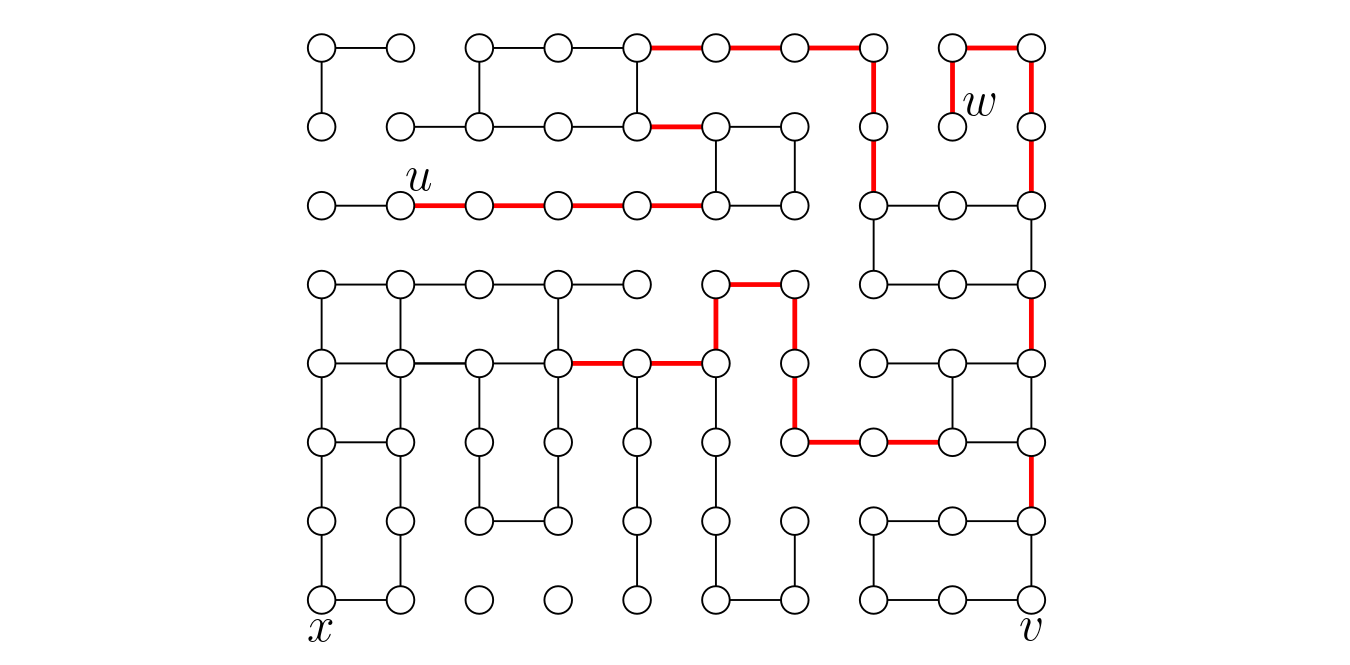
In this post, we'll solve a graph problem that comes up in the Wall Game.
See also the related, but harder, Double-Edge Cut Problem.
The single-edge cut problem
You are given an undirected, unweighted, connected graph G with V nodes and E edges, where each node is identified by an integer from 0 to V-1. You are also given a list, bonded_pairs, of k pairs of nodes.
We say an edge is essential if removing it from G disconnects a bonded pair.
Return a list of the essential edges.
Example:
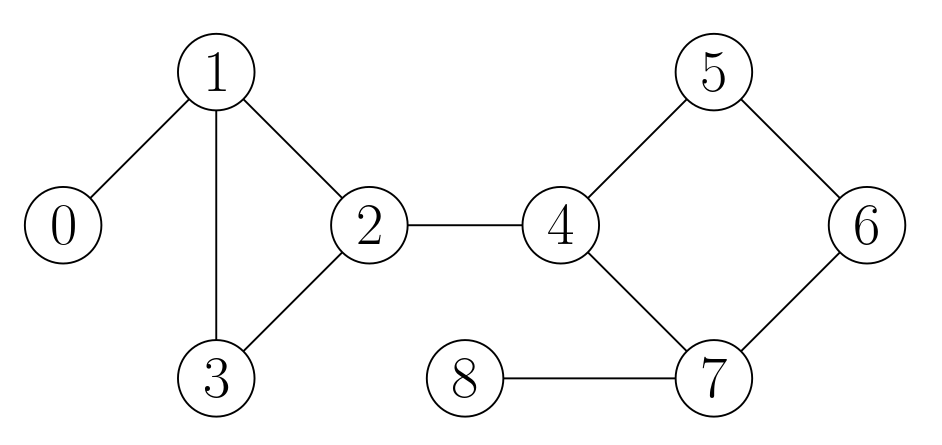
Given this graph and the list bonded_pairs = [[0, 1], [1, 5], [5, 7]], the essential edges would be [[0, 1], [2, 4]]:
- removing the edge
[0, 1]disconnects the bonded pair[0, 1] - removing the edge
[2, 4]disconnects the bonded pair[1, 5] - there is no way to disconnect the bonded pair
[5, 7]
Motivation
This is the key problem behind whether a wall can be added or not in the Wall Game. The board of the Wall Game may look something like the picture on the left:
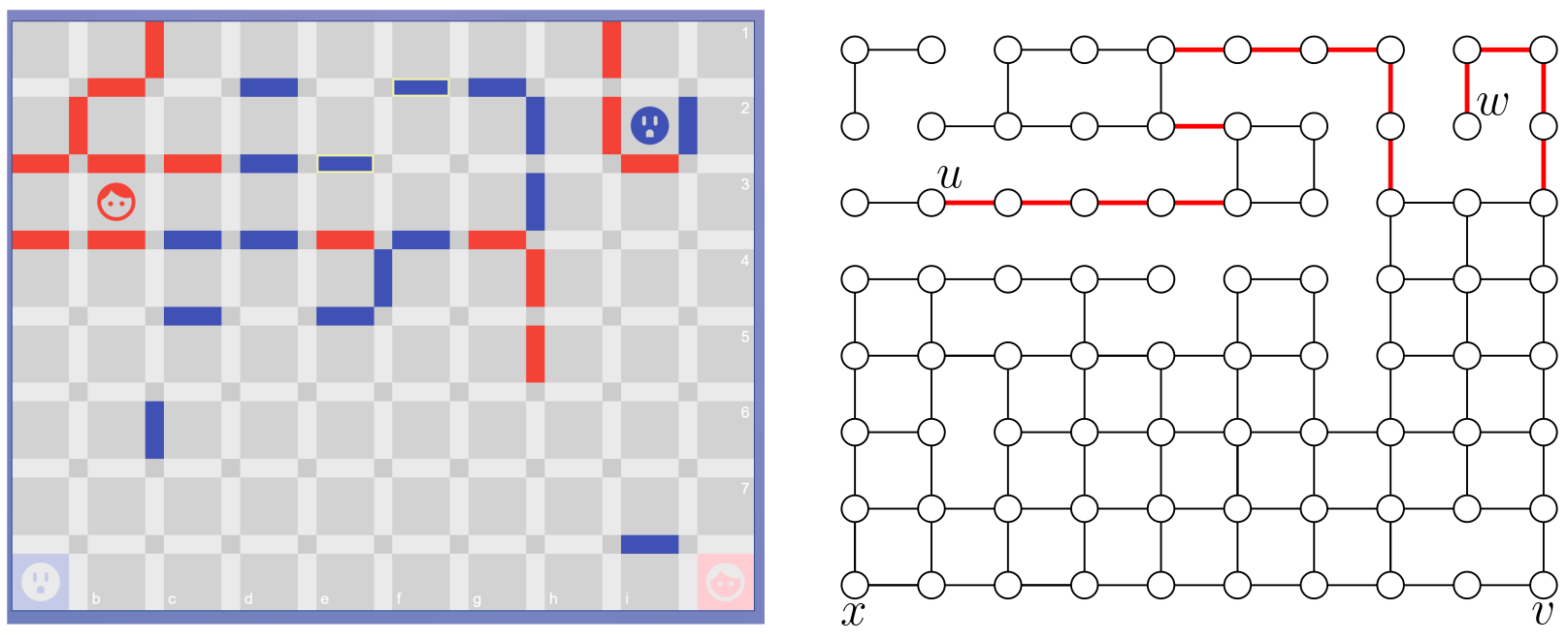
The right picture is the board modeled as a graph. The cells become nodes and two adjacent nodes are connected if there is no wall between them.
Players can build walls anywhere, which is like removing an edge. The only constraint is that they cannot fully block the opponent's path to their goal (or their own). Thus, each player and its goal form a bonded pair, and the essential edges are the walls that cannot be placed.
In the picture, the bonded pairs are [u, v] and [w, x], and the essential edges are shown in red.
Imagine that we want to implement a feature in the Wall Game website where, when you hover over a wall slot, it is highlighted in red if the move is invalid. To do this, we need to solve the single-edge cut problem. Beyond that, it could also be useful to program an engine, which needs to consider lots of moves.
Note: the graph from the Wall Game may not be connected (see, e.g., the isolated connected component in the top-left corner)--all we are guaranteed is that each bonded pair is in the same connected component. In this blog post, we assume the graph is connected for simplicity, but it is not hard to extend the algorithm to the disconnected case. We just do an initial pass to find all the connected components, and then process each one separately.
Why do we frame the problem in terms of k pairs, and not just two? There are variants of the Wall Game with more than two players:

In this 4-player variant, Player 1 needs to catch Player 2 before they themselves are caught by Player 4, Player 2 needs to catch Player 3 before they are caught by Player 1, and so on. We can think of it as having four bonded pairs.
Brute force solution
The naive solution is to consider each edge individually.
For each edge e in E, we:
- Remove it from
G(we denote the resulting graph asG - {e}). - Find the connected components in
G - {e}. - If two bonded nodes are in different connected components,
eis essential.
Step (1) takes O(1) time, Step (2) takes O(E) time (it can be done with a DFS or a BFS), and Step (3) takes O(k) time.
The total runtime is O(E * (E+k)).
Efficient solution
In this section, we'll solve the problem in O(E * k) time. In the next section, we'll see a more complicated but optimal O(E + k) algorithm.
We'll build up to it with a series of definitions and intermediate steps.
- Definition: In a connected graph, a bridge is an edge which, if removed, disconnects the graph.
In the example above, the bridges are [0, 1], [2, 4], and [7, 8].
- Definition: Given a pair of nodes in a connected graph,
sandt, an st-bridge is an edge which, if removed, disconnectssandt.
In the context of our problem, an edge is essential if it is an st-bridge for some bonded pair [s, t].
- Observation 1: Every
st-bridge is a bridge, but not necessarily the other way around. - Observation 2: Given two nodes,
sandt, take any path between them,P. Everyst-bridge must be inP.
Observation 2 is because if we remove any edge not in P, s and t will still be connected via P.
- Main result: Let
Pbe any path betweensandt. An edge is anst-bridge if and only if it is both a bridge and inP.
We can now formulate an algorithm based on this property:
Input: G (adjacency list), bonded_pairs (list of node pairs)
Output: set of essential edges
Find all the bridges in G
For each bonded pair [s, t]:
Find a path P between s and t
For each edge in P:
If it is a bridge:
Add it to the set of essential edges
We can find all the bridges in O(E) time using Tarjan's algorithm. We can find each path using DFS or BFS in O(E) time (interestingly, it doesn't matter how you find the path, as it can be any path). The total runtime is O(E + k * E) = O(E * k).
Here's a TypeScript implementation.
Optimal algorithm
If k is small, as in the Wall Game, the above algorithm is the most practical.
In this section, we'll see a linear-time (O(E + k)) algorithm, which is asymptotically optimal for any k.
The bottleneck of the previous algorithm is finding the k paths between bonded pairs. To achieve linear time, we need to do this in a single pass.
The key property we'll use is that, in Observation 2 above, we can choose any path between each bonded pair. We can start by finding a spanning tree T of G, and focus only on the paths connecting the bonded pairs through T. We can find a spanning tree in O(E) time using a DFS or a BFS (it doesn't matter).
It will be convenient to think of T as a rooted tree, so that we can talk about node depths and lowest common ancestors. We can root it at any node.
The root is at depth 0, its children are at depth 1, and so on. The lowest common ancestor of a pair of nodes u and v in T, denoted LCA(u, v), is the node in T that is an ancestor of both nodes and has maximum depth.
Recall that we want to identify all the edges in T that form paths between pairs of bonded nodes. Between any pair of nodes u and v, there is a unique path in T: the path that goes from u up to LCA(u, v) and from there down to v (note that LCA(u, v) could be u or v itself).
We can start by finding the LCA of each bonded pair in T. We can do this in linear time using Tarjan's off-line lowest common ancestors algorithm.
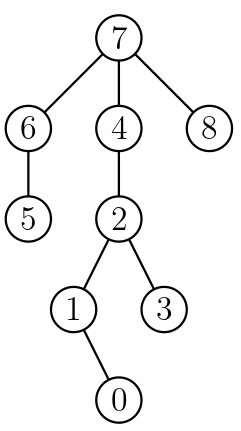
Here is a tree for the example graph from above, rooted at 7:
Henceforth, we say that a node u is bonded if it is bonded to at least one other node.
For each bonded node u, we define min_lca(u) as follows: among the LCA's of all bonded pairs involving u, min_lca(u) is the one with minimum depth.
For example, imagine that, in the tree above, node 1 is involved in 3 bonded pairs: [1, 3], [1, 0], and [1, 4]. The corresponding LCA's are 2 (at depth 2), 1 (at depth 3), and 4 (at depth 1). Of those, the one with minimum depth is 4, so min_lca(1) = 4.
The following observation characterizes the essential edges in terms of T:
- Observation 3: A bridge of
Gis essential if and only if it is between a bonded nodeuandmin_lca(u).
On the one hand, if we removed a bridge between u and min_lca(u), the bonded pair consisting of u and the node v such that LCA(u, v) = min_lca(u) will become disconnected. On the other hand, if a bridge is not between any bonded node u and min_lca(u), every bonded pair has a path that doesn't go through it, so it is not essential.
The idea behind our linear-time algorithm is to do a traversal through T. At each node u, we want to find the LCA with minimum depth among all the bonded pairs with one node in subtree(u) (the subtree rooted at u), if any. That is, we want to find the minimum-depth node in T that is the min_lca(v) for some node v in subtree(u). We actually only care about its depth, which we call subtree_min_lca_depth(u). We can compute subtree_min_lca_depth(u) recursively, aggregating the results from each child as well as the depth of min_lca(u) itself if u is bonded:
subtree_min_lca_depth(u) = min(
depth(min_lca(u)) if u is bonded, infinity otherwise,
subtree_min_lca_depth(v) for all v in children(u)
)
Finally, we can write a simple check for whether an edge in T is essential:
- Observation 4: If
[w, u]is an edge inT, wherewis the parent ofu,[w, u]is essential if and only if (1)[w, u]is a bridge inGand (2)subtree_min_lca_depth(u) < depth(u).
Condition (2) says that there is some node in the subtree rooted at u that is bonded to a node somewhere above u.
Here is the full pseudocode:
Input: G (adjacency list), bonded_pairs (list of node pairs)
Output: set of essential edges
Find all the bridges in G
Build a DFS tree T of G rooted at any node
Find the LCA of each bonded pair in T
Compute depth(u) for every node u in T
Compute min_lca(u) for each bonded node u
Do a post-order traversal through T as follows:
At each node u:
visit children recursively
if u is the root:
return
compute subtree_min_lca_depth(u) using the formula above
w = parent of u
if [w, u] is a bridge in G and subtree_min_lca_depth(u) < depth(u):
mark [w, u] as essential
As mentioned, finding bridges takes O(E) time, building a spanning tree takes O(E) time, and finding all k LCA's takes O(V + k) time; the remaining steps, including the main tree traversal, take O(V) time. Considering that the graph is connected, and thus V <= E, the total runtime is O(E + k).
Want to leave a comment? You can post under the X post.