Computational Aspects of Gerrymandering
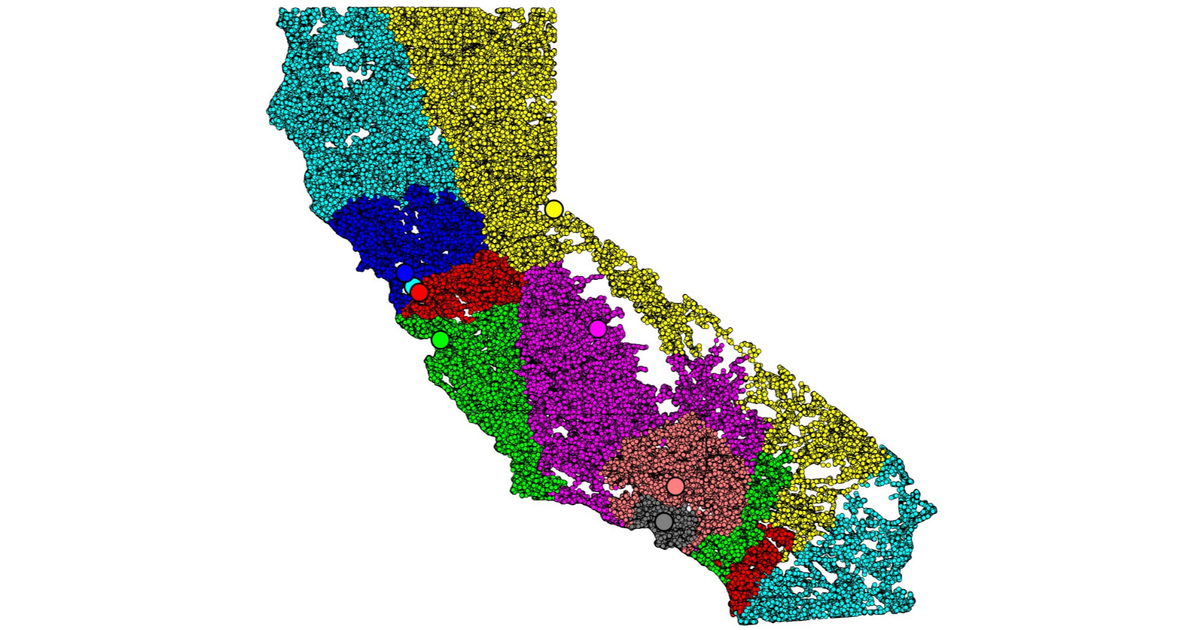
A potential solution to gerrymandering is using geometric, "politically-agnostic" algorithms to draw fair districts. At least, that's the premise of a line of research I followed in my PhD.
In this post, I will list a few reasons why this premise is flawed:
- The problem with gerrymandering as a math problem.
- Who gets to choose the algorithm?
- Dealing with self-gerrymandering.
- Benign gerrymandering?
My research explored the use of stable matching to define fair districts. I won't touch on it here, but I can spoil that we didn't find a satisfying solution. If you are interested, see Chapter 7 of my dissertation.
Background: What is gerrymandering?
Let's take the example of the US Congress. Each state is divided into a number of congressional districts proportional to its population (California has the most, with 52), and then each district elects one representative to Congress by majority vote.
The point of district representatives is local representation: they are supposed to represent the interests of the people in their district at the national level.
The problem is that how the district lines are drawn can completely change who wins, even if nothing else changes.
So, who gets to draw the districts? This process, called redistricting, happens every 10 years, after the census. Some states use independent commissions, but it's usually up to the state's incumbent party.
And that's where gerrymandering happens. The people drawing the districts -- often partisan -- have a good sense of how each area votes (based on voter records) and can shape the districts to favor their own party.
Gerrymandering happens in two ways:
- Cracking: forming districts where the favored party wins by a small margin, and
- Packing: forming districts where the opposing party wins by a large majority.
Packing is a way to "waste" opposing votes on districts that are already projected to be lost. Since a simple majority vote is used within each district, a party doesn't gain anything by winning with a wider margin.
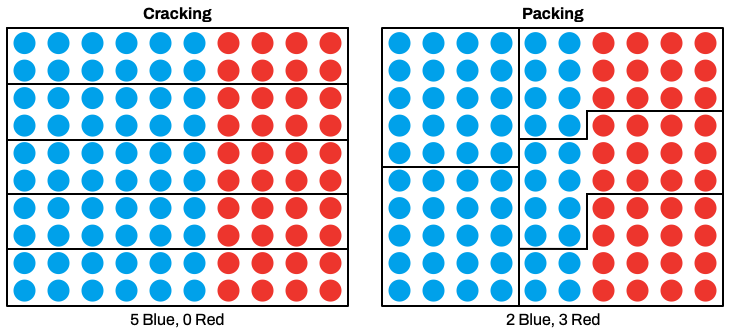
This graph shows how, without changing any votes, and keeping all the districts exactly the same size, the boundaries drawn can produce wildly different outcomes.
Yeah, it's bad.
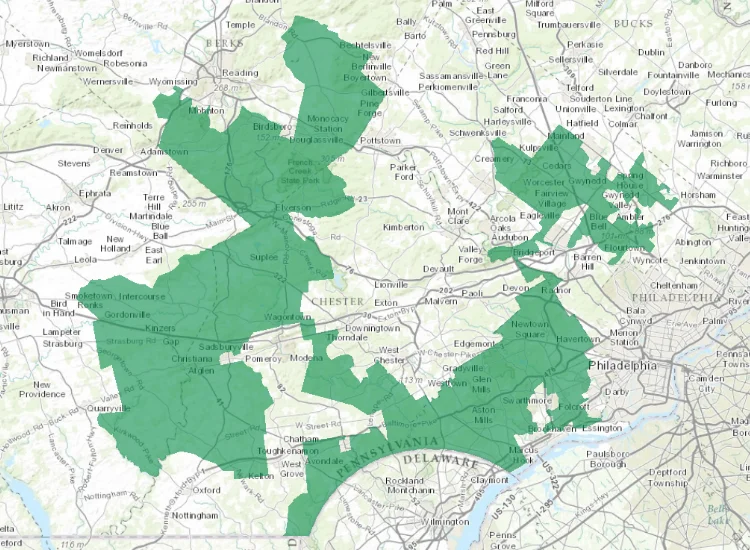
In practice, gerrymandered districts may look something like this:
The problem with gerrymandering as a math problem
To use an algorithm to draw fair districts, we first need to define a metric to optimize for. "Ideal" districts have two properties:
- Population balance: All the districts in a state have roughly the same population.
- Compact: Informally, districts should look more like a circle than an octopus.
The problem is that there is no objective way to turn this intuition into an objective function.
There are many geometric ways to measure the compactness of a district, such as:
- The ratio between the perimeter and the area of the district.
- The ratio between the area of the district and the area of its smallest enclosing circle.
This page lists 10+ compactness metrics. This page illustrates some of them.
Measuring whether districts are balanced is a bit more straightforward, but there's still room for interpretation: is it better if many districts are slightly unbalanced, or if one district is very unbalanced?
Then, there's the question of how to handle trade-offs between compactness and population balance. And the question of how to deal with natural geographic features that may justify weird district shapes.
In any case, districts obtained by optimizing for ANY reasonable objective function will be far better than gerrymandered ones, so, are we getting lost in inconsequential details?
But it actually matters when you consider this question:
Who gets to choose the objective function?
Each choice you make about the objective function will benefit one party more than the other.
You can't simply say, "We'll choose the most correct option," because there is no most correct geometric definition of compactness. It's intrinsically subjective.
Who gets to choose the algorithm?
Say we all agreed on an objective function.
For problems like this, it is typically computationally intractable to find the optimal solution. Certain formulations of redistricting have been shown to be NP-hard.
Instead, we need to rely on heuristics to get a "good enough" solution.
But then... we immediately run into the same problem:
Each choice you make about the algorithm will benefit one party more than the other.
Should we use a greedy algorithm? A genetic algorithm? Simulated annealing?
There are many heuristic algorithms.
And, once we choose an algorithm, how should we set its parameters? How long should we let it run for? If it involves randomization, how many times should we run it?
Even within the confines of an agreed objective function, there is still plenty of room for partisan manipulation -- likely enough to flip at least one district.
Unlike the problem of choosing the objective function, however, I think this problem has a non-partisan solution:
There should be a contest to find the district map that scores the highest on the objective function.
Both parties should be able to submit their own districts, whether drawn by hand or computed algorithmically, and the best one is chosen.
Both parties can try to optimize for their preferred outcomes, but they still need to outperform the other party's districts on the objective function. I'd even open the contest to the public, like a Kaggle competition for redistricting.
With this proposal, who gets to benefit the most from redistricting comes down to the parties' heuristic optimization skills, which is a strange point to land at, but it's better than one party choosing the algorithm.
Dealing with self-gerrymandering
Imagine a headline:
Republicans propose new redistricting plan where they get 65% of the seats with only 45% of the votes.
Is this proof of partisan gerrymandering?
Not necessarily.
There is a well-known phenomenon: Democrats heavily gravitate to big cities, effectively packing themselves into a few districts.
In this paper, the authors did Florida redistricting simulations using voter data from the 2000 presidential election. The election was nearly tied (Bush won by 537 votes, out of a total of 5,825,043 votes cast), so, ideally, each party would get around 50% of the seats.
They did hundreds of simulations generating randomized districts.
Every single time, the outcome favored Republicans.
They did simulations with different numbers of districts; they did simulations both optimizing and not optimizing for compactness; the result was the same.
Among all of the randomly simulated plans consisting of 25 districts (U.S. Congressional delegation), 40 districts (Florida Senate), and 120 districts (Florida House), not a single simulated plan produces at least as many Gore-leaning districts as Bush-leaning districts. Hence, both the compact and the non-compact simulation procedures are unable to produce a single Congressional, Senate, or House districting plan for Florida that is either neutral or pro-Democratic in its distribution of seats.
Benign gerrymandering?
Okay, so let's return to our ideal scenario, where we all agreed on the perfect objective function, and we had an open contest to find the district map that maximizes it. Then, we look at the map, and it turns out that one party is massively overrepresented.
What do we do?
It doesn't seem fair to just let it be, especially if this happens consistently in favor of one party across the country. Should a group be less represented for such an apolitical thing as liking big cities?
But, what's the alternative? Should we sacrifice district compactness in order to balance representation? Isn't that... gerrymandering?
Some kind of "benign" gerrymandering?
What a way to come full circle.
Perhaps purely geometric, "politically-agnostic" algorithms are not the answer. We could add a third factor to the objective function, in addition to compactness and population balance:
- Representation balance: Each party gets a number of seats roughly proportional to the number of votes they received.
On a related note, a type of gerrymandering called racial gerrymandering is sometimes done intentionally to ensure that minorities that would otherwise be "cracked" across multiple districts get some representation. Such districts are called majority-minority districts, and add yet more nuance to the issue of whether gerrymandering can (and should) be used for "good".
Conclusion
As a computer scientist, I still believe that algorithms can help us draw better districts. However, this post should illustrate why we can't completely eliminate human decisions from the process.
If you have any thoughts, please let me know!
Want to leave a comment? You can post under the linkedin post or the X post.