Problem Solving BCtCI Style

Here's a thought: You don't want the first time you think about the question "What should I do if I get stuck in a coding interview?" to be when you are stuck in a coding interview.

In a way, getting stuck in a coding interview is an opportunity. The main goal of the interview is to see your problem-solving thought process, and being stuck is the ideal time to showcase it.

But you want to be prepared. It's valuable to have a plan for this exact scenario. We all dread blanking out in an interview, but having a plan makes it easy to simply focus on executing it. So, let's talk about what such a plan could look like in this blog post.

In Beyond Cracking the Coding Interview, we go over all the steps in an interview, and our best tips to do well in each of them:

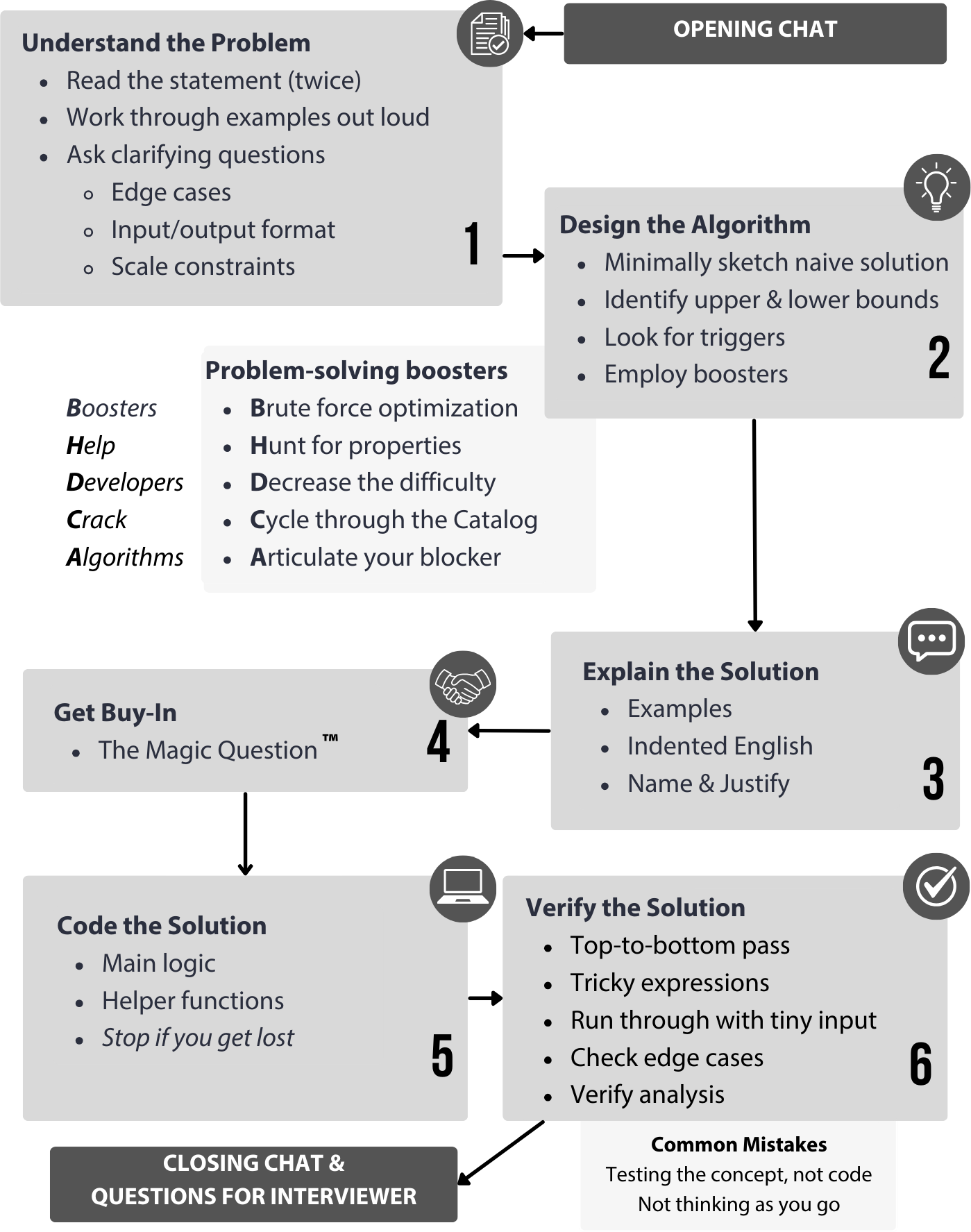
In this blog post, I'll zoom in on the problem-solving step, "Design the Algorithm," and illustrate the thought process with a problem.

As you can see, we break it down into four steps:

1. Minimally sketch the naive solution to establish a baseline.
2. Identify upper and lower bounds using big O analysis to narrow down the range of possible solutions.
3. Look for triggers (Keywords) that point to a specific approach.
4. Employ boosters: problem-solving strategies that give you the "boost" you need when you are stuck.

These are not revolutionary ideas -- it's what good problem solvers do and think about instinctively. One of the main goals of the book, and of this blog post, is to spell out the thought process of people who are really good at this in a relatable way so that anyone can reproduce it.

We playfully call this the MIKE template (Minimally sketch brute force, Identify bounds, Keywords (triggers), Employ boosters) after Mike Mroczka, one of the authors of BCtCI.

Rather than expanding on these now, we'll see them in action with the following problem.

Problem Statement

The problem is based on LeetCode 3458, which appeared in a recent contest. You can go and give it a try before reading on (it's labeled as medium, but I think it's on the harder end of medium). The thought process I'll walk through here is based on how I solved it during the contest.

Given a string s, a substring of s is special if any character in it does not appear outside it.

For example, if s is "abcba":

• "bcb" is a special substring because 'b' and 'c' do not appear in s outside "bcb".
• "abc" is not a special substring because 'a' appears in s outside "abc".

Given a string s consisting of n lowercase English letters, determine the maximum number of disjoint special substrings. Two substrings are disjoint if they do not overlap.

Example 1: s = "abcba"
Output: 1
The special substrings are "abcba", "bcb", and "c". They all overlap with each other, so we can only pick 1.

Example 2: s = "banana"
Output: 2
The special substrings are "b", "banana", and "anana". We can pick "b" and "anana".

Constraints:

• 2 <= n <= 10^5
• s consists only of lowercase English letters.

Digesting the problem

First, we need to digest what the problem is asking. This problem follows a common pattern: it introduces a kind of esoteric definition, "special substring", and then asks us to do something with it.

To make sure we understand what a special substring is, it's good to look at a few examples, starting with the provided ones. For instance, in "abcba", do you understand why "a" is not special but "c" is?

Take some time to come up with your own examples. Rushing to solving a problem before understanding it well is a common but often costly mistake.

Approach

Sometimes, it helps to tackle just one part of the problem first, so we can start making progress.

We can think of an algorithm with 2 parts:

• Part A: Find all the special substrings.
• Part B: Find the most non-overlapping special substrings.

Let's start with part A.

Part A: Find all the special substrings

We'll walk through the MIKE template.

M: Minimally sketch brute force

The key here is to not overthink it. We just want to get the ball rolling and have a baseline we can improve upon.

Since we don't want to spend too much time in an interview, you could even just describe the idea in a sentence and move on. But we prefer to briefly sketch it in very high-level pseudocode. We call it 'intended English': it's written like English, but with indentation to show the code structure:

Algo 1: brute force
T: O(n^4)
for each possible substring start
  for each possible substring end
    # check if it is special
    for each letter inside the substring
      for each letter outside the substring
        if they match, it is not special

In this case, the space complexity depends on how many special substrings we might find, which is not clear yet, so we'll leave it out for now.

I: Identify upper and lower bounds

We can use big O analysis to narrow down the range of possible solutions. An upper bound means "we don't have to consider any solution that takes longer than this", and a lower bound means the opposite: "we don't have to consider any solution that takes less time than this". In the book, we go over two ways of establishing an upper bound and two ways of establishing a lower bound:

Upper bounds:

• Brute force upper bound: we just saw that we can find all special substrings in O(n^4) time, so we don't have to consider any solution that takes longer than that.
• TLE (Time Limit Exceeded) upper bound: here is where we use the problem constraints to establish an upper bound. The problem says that n <= 10^5, which usually means that O(n^2) solutions are too slow, but O(n log n) or faster solutions are fine.

Lower bounds:

• Output-size lower bound: the space taken by the output is a lower bound for the time complexity, because that's how long it takes just to write the output. In our case, the output of the overall problem is just a number, so this lower bound is trivial: O(1). Bounds are not always useful!
• Task-based lower bound: some problems involve an inherent task that any solution must fulfill. The runtime of this task is a lower bound. In this case, we know we at least need to read every letter in the input, so we have a lower bound of O(n). In other words, we can rule out solutions that take O(log n) or O(1) time.

Combining our findings, we can narrow down our search range to O(n log n) or O(n) algorithms (something like O(n log^2 n) would also be fine, it's just less common).

K: Keywords (triggers)

There are certain properties of problems that point to a specific approach. Here are some triggers we can identify for this problem:

• finding substrings -> sliding windows
• O(n log n) possible target complexity -> sorting or heaps

Unfortunately, triggers are not a guarantee, and these triggers don't seem to help for this problem:

• In sliding windows, once you move past a character, you don't later go back. So, in Example 1, it would be impossible to find both "abcba" and "bcb": if you find "abcba" first, the right pointer would have to go back to find "bcb". But if you find "bcb" first, the left pointer would have to go back to find "abcba".
• Sorting doesn't seem like a good fit because the input order is important.

Do you think I missed any other triggers?

E: Employ boosters

So, triggers didn't help, and brute force is still far from the target complexity. It's time to employ boosters.

Here's an overview:

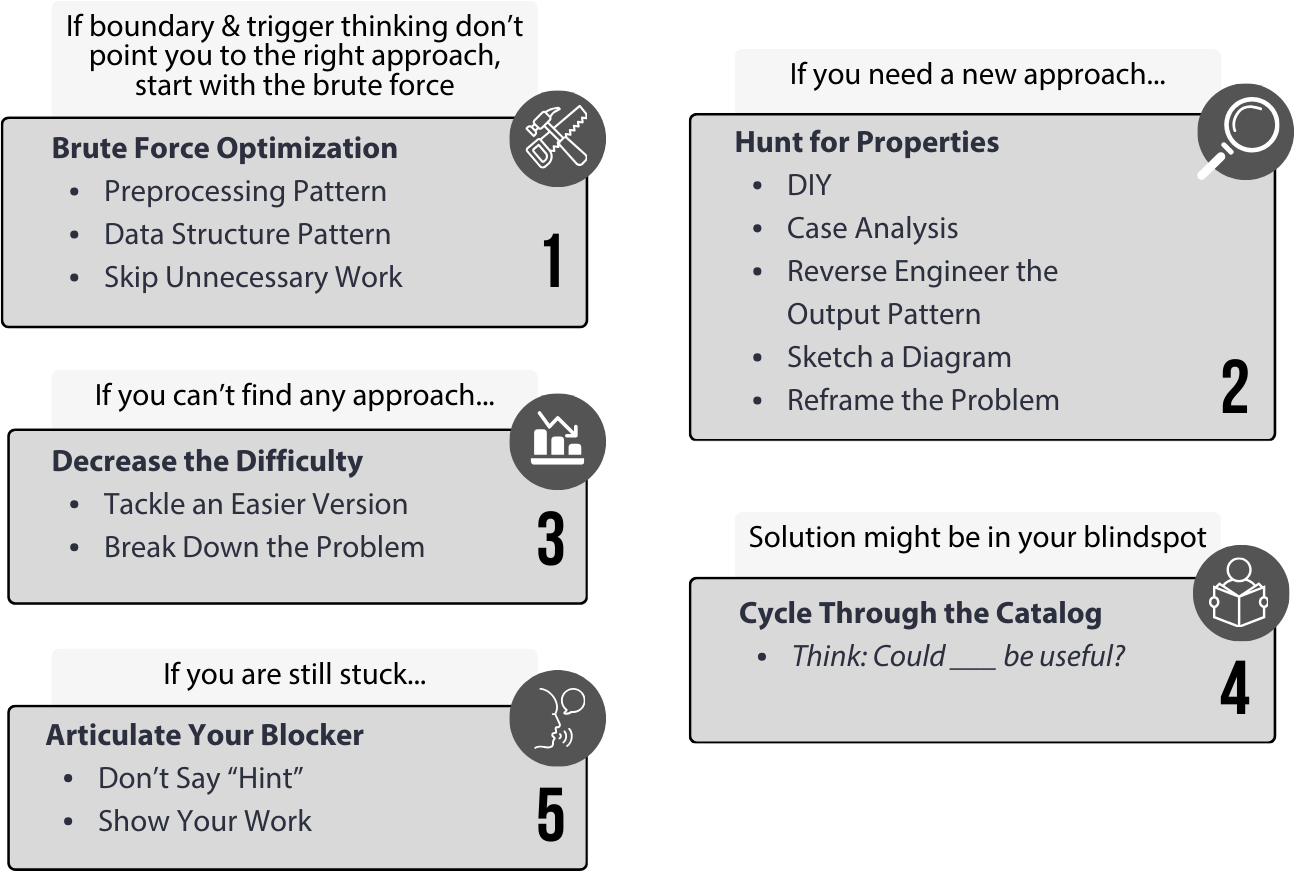
The boosters are roughly ordered, but we don't always have to use them in order. In fact, here's a plot twist: what we did at the beginning, splitting the problem into two parts, is the third booster: Decrease the Difficulty -> Break Down the Problem.

Booster 1: Brute force optimization

The first booster is straightforward: take the brute force pseudocode we already have and try to optimize it.

In the boosters diagram, we list three ways to go about it. One of them is the Data structure pattern. Many bottlenecks come from having to do some calculation inside a loop. In those situations, ask yourself,

"Do I know of any data structure which makes this type of operation faster?"

For this problem, we can use a hash set to optimize the innermost loop:

Algo 2: set optimization
T: O(n^3)
for each possible substring start
  for each possible substring end
    # check if it is special
    dump the substring into a set
    for each letter outside the substring
      if it is in the set, it is not special

Boster 2: Hunting for properties

We got down to O(n^3) time, but we know we still need to bring this down to the target complexity.

Let's say we don't know how to optimize the code further. Often, the breakthrough comes from uncovering some "hidden" observation or property not explicitly mentioned in the statement. Our second booster is to go hunting for those.

In the book, we discuss a bunch of ways of doing this, but the most basic and effective one is to try to solve the problem manually with a non-trivial example. By non-trivial, we mean that is is not some weird edge case, which would not be helpful for figuring out a general algorithm.

Let's actually do that: take s = "mississippi" and manually try to find all the special substrings.

Don't overthink it. Don't think about algorithms yet. Just write them down.

Done? Ok, now try to reverse-engineer what shortcuts your brain took. This is one property you may have noticed:

Property 1

Property 1: a special substring must start at the first occurrence of a letter.

You may have noticed this property when your brain skipped over the second, third, or fourth 'i's in mississippi and intuitively realized that there is no special substring starting at those. Writing down the property formalizes this instinct and ropes in the interviewer.

Now that we have a property, we have to find a way to use it. Property 1 allows us to optimize the outer loop: it means we only have 26 = O(1) possible starts to check (problems where the input consists of only lowercase letters often have optimizations like this).

As we iterate through the possible starts, we can track letters seen so far (e.g., in a hash set):

Algo 3: selective start
T: O(26 * n^2) = O(n^2)
for each possible substring start i
  if seen s[i] before
    continue
  add s[i] to seen set
  for each possible substring end
    # check if it is special
    dump the substring into a set
    for each letter outside the substring
      if it is in the set, it is not special

We haven't hit our target time complexity yet, so let's keep hunting for properties. Here is another one:

Property 2

Property 2: of all the special substrings that start at a given letter, we only care about the shortest one.

Our ultimate goal is to find the most non-overlapping special substrings. If we can choose between two special substrings, one of which contains the other, it is always "optimal" or, at least, "safe" to pick the smaller one.

For instance, if s is "baa", we have two choices for special substrings starting at 'b': "baa" and "b". We should pick "b" so that the "aa" part can be in another disjoint special substring.

Again, when we find a property, we need to think of how to apply it. Property 2 means that, for each starting point i, we can grow a substring one letter at a time, and stop as we find the first special substring.

Let's break this down a bit more: say you start at index i.

• If you find a letter c that appears at some later point, we need to grow the substring up to that index.
• If you find a letter c that appears before i, we can stop the search. No substring starting at i can be special.

For example, imagine i starts at the first 'b' in the following string:

"abbbbbabbba"
  ^
  i

That means we need to grow the substring at least up to the last 'b' in the string:

"abbbbbabbba"
  ^       ^
  i   need to grow up to here

As we grow the substring, we hit an 'a', which appears before i, and we realize that no substring starting at i can be special.

"abbbbbabbba"
  ^    ^
  i invalid

We can now add this logic to our algorithm. We can start the algorithm by computing the first and last index of each letter (this is an example of the preprocessing pattern in the boosters diagram -- it's common for properties from Booster 2 to enable optimizations from Booster 1).

Then, as we grow each substring, we keep track of the farthest index we need to reach. (This is actually a common pattern in sliding window algorithms, where we maintain information about the window as it 'slides', rather than computing it form scratch every time the window moves. So, the 'sliding windows' trigger wasn't completely off).

Algo 4: smallest special substring
T: O(26 * n) = O(n)
S: O(26 * n) = O(n)
preprocessing: compute the first and last index of each letter

for each possible substring start i
  for each index j starting at i
    if s[j] appears before i
      no special string starts at i
    else
      must_reach = max(must_reach, last occurrence of s[j])
    if j reached must_reach:
      s[i]...s[j] is a special substring (the shortest one starting at s[i])

We got the time down to O(n). Since we hit the lower bound, we can be confident Part A is as good as it can be, and we can move on to Part B.

Part B: Find the most non-overlapping special substrings

Let's be honest: even if in the book we really emphasize developing your problem-solving skills by using the MIKE template and the boosters, knowing a bunch of leetcode questions DOES give you an edge in coding interviews. So, I'll tell you how I actually solved this problem in the contest. I realized that Part B is just a variation of a classic greedy problem: most non-overlapping intervals. Indeed, a substring can be seen as an interval of the string.

The "most non-overlapping intervals" problem is in BCtCI, so I already knew that it can be solved with a greedy algorithm that sorts the intervals by their end time and then iterates through them, picking the ones that don't overlap with the previous one (here is a similar problem on leetcode). This algorithm fits within our target time complexity, so I didn't have to think beyond that.

If I didn't already know the solution, I would have walked through the MIKE template again for Part B.

Full implementation

Here is a full implementation:

# T: O(26 * n) = O(n)
# S: O(26 * n) = O(n)
def select_k_disjoint_special_substrings(s):
    special_substrings = find_special_substrings(s)  # Part A
    return most_non_overlapping_intervals(special_substrings)  # Part B

def find_special_substrings(s):  # Algo 4
    # Preprocessing: compute the first and last index of each letter
    first_idx = {}
    last_idx = {}
    for i, char in enumerate(s):
        if char not in first_idx:
            first_idx[char] = i
        last_idx[char] = i

    special_substrings = []
    for i in range(len(s)):
        if i != first_idx[s[i]]:
            continue

        must_reach = i
        for j in range(i, len(s)):
            if first_idx[s[j]] < i:
                break
            must_reach = max(must_reach, last_idx[s[j]])

            if j == must_reach:
                special_substrings.append((i, j))
                break

    return special_substrings

def most_non_overlapping_intervals(intervals):  # Classic Greedy
    intervals.sort(key=lambda x: x[1])  # Sort by endpoint
    count = 0
    prev_end = -math.inf
    for l, r in intervals:
        if l > prev_end:
            count += 1
            prev_end = r
    return count

You may think that the bottleneck is the sorting, but it's not. Recall that there are only up to 26 special substrings (by Property 1). Sorting 26 intervals takes O(26 log 26) = O(1) time.

Conclusion

I wanted to give an overview of all the high-level ideas for problem-solving in leetcode-style interviews. We could dive a lot deeper into any of those ideas, so this blog post may feel a bit rushed, but the meta-point is that you should have a plan for when you are stuck in an interview (and you should be following it during your practice sessions so it becomes second nature). It's not important that you use the MIKE template -- your plan should work for you. But the ideas covered in this post should probably be part of it.

If you have any comments, let me know on linkedin or X.