BCtCI Chapter: Monotonic Stacks & Queues

This is a free, online-only chapter from Beyond Cracking the Coding Interview, co-authored with Gayle Laakmann McDowell, Mike Mroczka, and Aline Lerner. I'm crossposting the chapter here as the primary author.
You can try all the problems from this chapter with our AI interviewer at bctci.co/monotonic-stacks-and-queues. You can also find full solutions in Python, C++, Java, and JS there.
This is a Tier 3 DS&A topic. The book contains all the Tier 1 & 2 topics. You can find other Tier 3 topics online at bctci.co (Part VIII of the ToC).
Report bugs or typos at bctci.co/errata.
Prerequisites: Stacks & Queues, Sliding Windows. It is recommended to review those chapters from BCtCI before reading this one.
Introduction
We covered stacks and queues in the Stacks & Queues chapter. Stacks have LIFO (last-in-first-out) behavior, while queues have FIFO (first-in-first-out) behavior.
In this chapter, we'll cover an advanced variation known as monotonic stacks and queues (and deques).
We'll assume the following APIs:
| Stack | Description | Queue | Description | Double-ended queue (deque) |
|---|---|---|---|---|
push(val) | Push to top | push(val) | Push to front | push_front(val) |
pop() | Pop from top | pop() | Pop from back | pop_front() |
peek() | Peek top | peek() | Peek back | peek_front() |
size() | size() | push_back(val) | ||
pop_back() | ||||
peek_back() | ||||
size() |
With standard implementations described in the Stacks & Queues chapter, all these operations take constant time (or amortized constant time in the case of dynamic-array-based implementations).
Max Queues
A "max queue" is a queue variation that tracks the maximum element in the queue. This operation can be really useful to solve certain problems we'll see later in this chapter, so it's useful to know how to implement it on the spot. As we'll see, the core technique to make max queues efficient is using a monotonic deque. Let's start with a data structure design question about how to implement a max queue.
Problem 1: Max Queue
Try it yourself →Implement a MaxQueue class that behaves like a normal queue but also supports a max() operation. This operation returns the maximum of the elements in the queue without modifying the queue.
In total, the operations are:
push(val): Add an element to the back of the queue.pop(): Remove and return the element at the front of the queue.peek(): Return the element at the front of the queue.max(): Return the maximum element currently in the queue.size(): Return the number of elements in the queue.
Guidelines:
- All the operations should take constant time (amortized constant time is fine).
- You can use your language's built-in queue and deque data structures (or assume you have them available if your language doesn't provide them).
- For simplicity, you can assume that
pop(),peek(), andmax()are never called on an empty queue. - You can assume that the queue will only contain integers.
Example:
MaxQueue operations Queue elements
q = MaxQueue() []
q.push(10) [10]
q.push(30) [10, 30]
q.push(20) [10, 30, 20]
q.max() // Returns 30. [10, 30, 20]
q.pop() // Returns 10. [30, 20]
q.max() // Returns 30. [30, 20]
q.pop() // Returns 30. [20]
q.max() // Returns 20. [20]
q.push(50) [20, 50]
q.push(30) [20, 50, 30]
q.push(20) [20, 50, 30, 20]
q.push(10) [20, 50, 30, 20, 10]
q.max() // Returns 50. [20, 50, 30, 20, 10]
q.push(50) [20, 50, 30, 20, 10, 50]
q.max() // Returns 50. [20, 50, 30, 20, 10, 50]
q.pop() // Returns 20. [50, 30, 20, 10, 50]
q.pop() // Returns 50. [30, 20, 10, 50]
q.max() // Returns 50. [30, 20, 10, 50]
Solution 1: Max Queue
Full code & other languages →Our MaxQueue class is built on top of a regular (internal) queue, which we'll call queue. Push, pop, peek, and size operations all operate on queue, as usual.
The naive solution for max() would be to traverse the queue every time we need to find the maximum element. This would take linear time, which is too slow.
The next thought is to precompute the max. We could have a cur_max variable with the maximum element, which allows us to answer max() in constant time. However, this variable would need to be updated whenever we push or pop an element from the queue. A push is easy to handle: we just need to compare the new element with cur_max and update it if necessary. A pop is more difficult: if we remove the maximum value, we need to do a linear scan to find the new maximum.
Keeping track of the current maximum is the right idea, but we need an approach that is a bit more sophisticated:
- Keep track of the current maximum,
cur_max. - Keep track of the maximum among the elements after
cur_max:after_max. - Keep track of the maximum among the elements after
after_max:after_after_max. - And so on.
This way, when we pop the current maximum, we can immediately find the next maximum.
We might need any number of "next maximums," so we need some kind of data structure to keep track of them:
[cur_max, after_max, after_after_max, after_after_after_max, ...]
For example, if queue is [20, 50, 30, 40, 10], then the data structure is [50, 40, 10].
With this data structure, which we'll call a monotonic decreasing deque for reasons we'll see later, we can answer max() in constant time: just return the first element. The hard part is how to maintain it as we push and pop elements from queue.
What can we say about this data structure?
- It is decreasing:
cur_max >= after_max >= after_after_max >= ... - Its elements are in the same order as in
queue. - It starts with the maximum element in
queue. - It ends with the last element in
queue(if we pop every element except the last one, the last one becomes the maximum).
Pay attention to all these properties by looking at the following example:
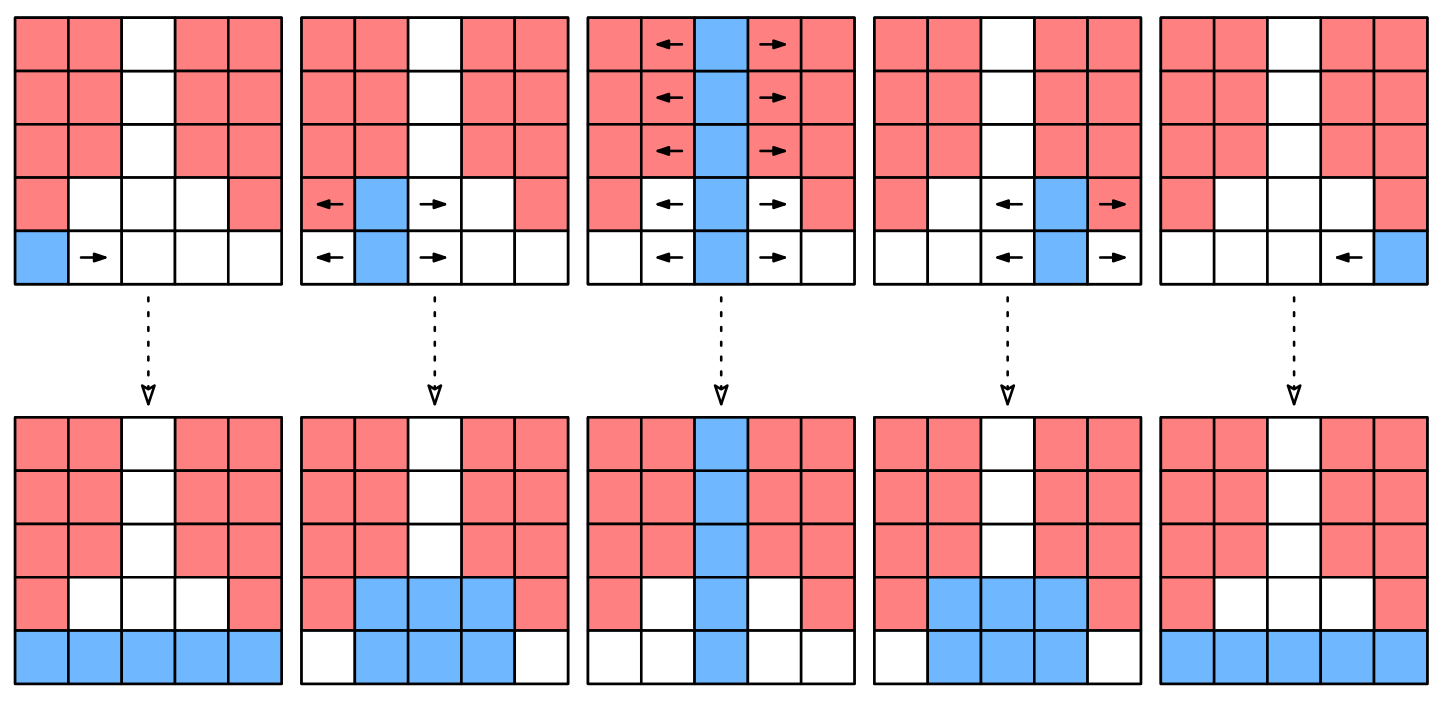
MaxQueue operations internal queue mono_decr_deque
q = MaxQueue() [] []
q.push(10) [10] [10]
q.push(30) [10, 30] [30]
q.push(20) [10, 30, 20] [30, 20]
q.max() // Returns 30. [10, 30, 20] [30, 20]
q.pop() // Returns 10. [30, 20] [30, 20]
q.max() // Returns 30. [30, 20] [30, 20]
q.pop() // Returns 30. [20] [20]
q.max() // Returns 20. [20] [20]
q.push(50) [20, 50] [50]
q.push(30) [20, 50, 30] [50, 30]
q.push(20) [20, 50, 30, 20] [50, 30, 20]
q.push(10) [20, 50, 30, 20, 10] [50, 30, 20, 10]
q.max() // Returns 50. [20, 50, 30, 20, 10] [50, 30, 20, 10]
q.push(50) [20, 50, 30, 20, 10, 50] [50, 50]
q.max() // Returns 50. [20, 50, 30, 20, 10, 50] [50, 50]
q.pop() // Returns 20. [50, 30, 20, 10, 50] [50, 50]
q.pop() // Returns 50. [30, 20, 10, 50] [50]
q.max() // Returns 50. [30, 20, 10, 50] [50]
Finally, let's talk about how to maintain the monotonic decreasing deque as we push and pop elements from the queue.
Pop is straightforward: if the element we pop from the queue is the maximum, we also pop it from the monotonic deque.
Push is the tricky one: if we push x, before adding x to the monotonic deque, we iteratively remove elements from the back of the monotonic deque that are smaller than x, since they can never be the maximum.
For instance, if mono_decr_deque = [50, 30, 20, 10] and we push 40, we iteratively pop 10, 20, and 30 until we get mono_decr_deque = [50], and then we add the new element.
Now, it finally makes sense to call this data structure a monotonic decreasing deque: it is a deque (a double-ended queue) because we need to remove elements from both ends: from the front during pop() and from the back during push(). "Monotonic decreasing" simply means that the elements are in decreasing order, which results from how we push elements to it.
Here is the implementation:1
class MaxQueue:
def __init__(self):
self.queue = Queue()
self.mono_decr_deque = Deque()
def peek(self):
return self.queue.peek()
def size(self):
return self.queue.size()
def max(self):
return self.mono_decr_deque.peek_front()
def pop(self):
val = self.queue.peek()
# Check if we are popping the max
if val == self.mono_decr_deque.peek_front():
self.mono_decr_deque.pop_front()
self.queue.pop()
return val
def push(self, val):
self.queue.push(val)
# Remove elements from the monotonic deque that can never be the max
while not self.mono_decr_deque.empty() and self.mono_decr_deque.peek_back() < val:
self.mono_decr_deque.pop_back()
self.mono_decr_deque.push_back(val)
Analysis. We can rely on the fact that queue and deque operations take constant time. This means that all operations except push() take constant time, as they don't have any 'loops'.
But what about the loop in push()? In the worst case, it takes O(n) time, where n is the size of the queue. For instance, if we push 100, 99, 98, ..., 1, mono_decr_deque will have length 100. If we then push 101, we'll need to pop every single element from it.
What we can say is that push() takes amortized constant time. Recall the definition of amortized time from the 'Dynamic Arrays' chapter: what that means is that if we do n operations in total with our MaxQueue, the total time is O(n), which means that, on average, each operation takes constant time.
This is because each element is added to mono_decr_deque at most once and removed from it at most once. Therefore, the total time for all additions and removals is O(n).
We focused on the case of finding the maximum in the queue, but sometimes we need the minimum instead. The minimum case is symmetric—we just reverse the comparison inside push().
Max Queue Applications
In this section, we'll see problems that can be solved efficiently using a max queue. Similar to union-find problems, solving these questions involves 2 steps: (1) implement the max queue data structure (as we did in Problem 1), and (2) use it to solve the original problem.
The common theme to problems that can be solved with a max queue is that they involve some kind of sliding maximum. Problem 2 is the barebones version of the sliding maximum problem. We'll use it to understand the concept before getting into more advanced problems.
Problem 2: Sliding Window Max
Try it yourself →Given a non-empty integer array, arr, and a subarray size, k, find the maximum element in each subarray of size k, from left to right.
Example 1:
arr = [10, 20, 30, 40, 30, 20, 10], k = 2
Output: [20, 30, 40, 40, 30, 20]
Example 2:
arr = [10, 20, 30, 40, 30, 20, 10], k = 3
Output: [30, 40, 40, 40, 30]
Assume that 0 < k <= n, where n is the length of arr.
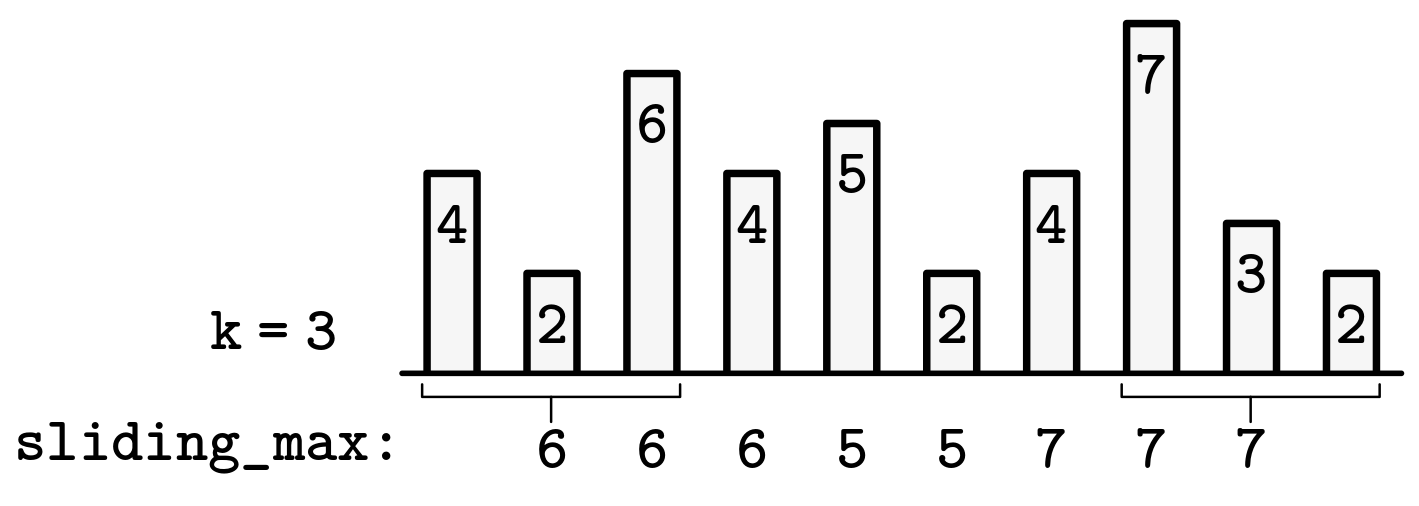
Solution 2: Sliding Window Max
Full code & other languages →The naive solution is to iterate over each subarray of size k and find the maximum element. This takes O(n * k) time.
We can do better with a sliding window. As we saw in the Sliding Windows chapter, the main question we should ask to implement a sliding window efficiently is:
"What information do I need about the window to check its validity and evaluation efficiently?"
In this case, we need to maintain the maximum as the window slides, which is the perfect use case for a 'max queue' (Problem 1). We usually need to implement the MaxQueue class ourselves, which we can do separately from the sliding window.
Returning to the main problem, this problem fits the 'fixed-length' window pattern, so we can use the fixed-length window recipe we saw in the Sliding Windows chapter:
def sliding_window_max(arr, k):
l, r = 0, 0
max_queue = MaxQueue()
res = []
while r < len(arr):
max_queue.push(arr[r])
r += 1
if r - l == k:
res.append(max_queue.max())
max_queue.pop()
l += 1
return res
Each MaxQueue operation takes amortized constant time, so the overall time complexity is O(n).
We could fold the monotonic deque logic of the max queue directly into the sliding_window_max function, but it's usually easier to break down problems like these into two tasks: implement the max queue, and then implement the sliding window.
Max queue problem set
Implement and use a max queue to solve the following problems.
Problem 3: Largest Temperature Change
Try it yourself →We are trying to install sensors that are sensitive to sudden temperature changes. The sensors should be fine as long as the temperature doesn't change too much within any k-day period.
Given an array temperatures with at least two integers, where each element represents the average temperature on a given day, and a number k with 2 ≤ k ≤ len(temperatures), return the maximum difference between average temperatures in a k-day period.
Example 1:
temperatures = [12, 13, 12, 13, 13, 12, 11, 12], k = 3
Output: 2
The 3-day period with the maximum difference is [13, 12, 11], which has a difference of 13 - 11.
Example 2:
temperatures = [10, 30], k = 2
Output: 20
Problem 4: Longest Stable Period
Try it yourself →We are planning an expedition, and we don't know exactly how many days it will take. Since we don't want to carry too many different types of clothes, we want to know the longest period of time when temperatures are stable, meaning that they don't change by more than t degrees. That will be the ideal time for our expedition.
Given an array, temperatures, with at least two integers, where each element represents the average temperature on a given day, and a number t, return the length of the longest subarray where the difference between the maximum and minimum temperature is at most t.
Example 1:
temperatures = [12, 16, 14, 15, 13, 17], t = 3
Output: 4
The longest stable period is [16, 14, 15, 13].
Example 2:
temperatures = [30, 10], t = 100
Output: 2
Example 3:
temperatures = [30, 10], t = 1
Output: 1
Problem set solutions.
Solution 3: Largest Temperature Change
Full code & other languages →The naive solution is to iterate over each subarray of size k and find the maximum and minimum elements. This takes O(n * k) time.
We can do better with a sliding window. We should ask: "What information do I need about the window to check its validity and evaluation efficiently?"
In this case, we need to maintain the maximum and minimum as the window slides, which is the perfect use case for monotonic deques. We'll implement and adapt the MaxQueue class we saw in Problem 1 to support both max() and min(). The idea to support min() is the same as max(): we just have a separate deque and flip the comparison operator in the push() method (you can see the full MaxMinQueue class online).
Returning to the main problem, we can use the fixed-length window recipe:
def largest_temperature_change(arr, k):
l, r = 0, 0
max_min_queue = MaxMinQueue()
res = -math.inf
while r < len(arr):
max_min_queue.push(arr[r])
r += 1
if r - l == k:
res = max(res, max_min_queue.max() - max_min_queue.min())
max_min_queue.pop()
l += 1
return res
Each MaxMinQueue operation takes amortized constant time, so the overall time complexity is O(n).
Solution 4: Longest Stable Period
Full code & other languages →The naive solution is to start from each day and see how far we can go while keeping the temperature stable. This takes O(n^2) time.
We can do better with a sliding window. We should ask: "What information do I need about the window to check its validity and evaluation efficiently?"
Like in the previous problem, we need to maintain the maximum and minimum as the window slides, so we can use a MaxMinQueue class.
Returning to the main problem, this problem fits the maximum window pattern, so we can use the maximum window recipe we saw in the Sliding Windows chapter. We grow the window when we can (i.e., adding temperatures[r] to the window doesn't make the window's temperatures unstable), and shrink when we must.
def longest_stable_period(temperatures, t):
l, r = 0, 0
max_min_queue = MaxMinQueue()
cur_best = 0
while r < len(temperatures):
can_grow = l == r or (max(max_min_queue.max(), temperatures[r]) - min(max_min_queue.min(), temperatures[r]) <= t)
if can_grow:
max_min_queue.push(temperatures[r])
r += 1
cur_best = max(cur_best, r - l)
else:
max_min_queue.pop()
l += 1
return cur_best
In sliding window problems (see the 'Sliding Windows' chapter), it is sometimes useful to be able to track the maximum (or minimum) in the window. We can use a monotonic deque to implement a 'max queue' (or 'min queue') and compute this information efficiently.
Next Greater Element (NGE)
Similar to monotonic deques, a monotonic stack is a stack in which the values are ordered, either increasing or decreasing. If repeated values are not allowed, the stack is strictly monotonic.
If max queues are the killer application of monotonic deques, the main application of monotonic stacks is computing the next greater element array. We'll define this array, see how to compute it with a monotonic stack, and then we'll use it to solve other problems.
Problem 5: Next Greater Element
Try it yourself →Given an array of integers, arr, return an array of the same length, NGE, such that NGE[i] is the first index j after i such that arr[j] > arr[i]. If there is no such j, then NGE[i] = -1.
Example 1:
Index: 0 1 2 3 4 5
arr = [5, 3, 10, 8, 8, 10]
Output: [2, 2, -1, 5, 5, -1]
Example 2:
Index: 0 1 2 3 4 5 6 7 8 9
arr = [4, 2, 6, 4, 5, 2, 4, 7, 3, 7]
Output: [2, 2, 7, 4, 7, 6, 7, -1, 9, -1]
Example 3:
Index: 0 1 2 3 4
arr = [5, 5, 5, 5, 5]
Output: [-1, -1, -1, -1, -1]
Example 4:
Index: 0 1 2 3 4
arr = [5, 6, 7, 8, 9]
Output: [1, 2, 3, 4, -1]
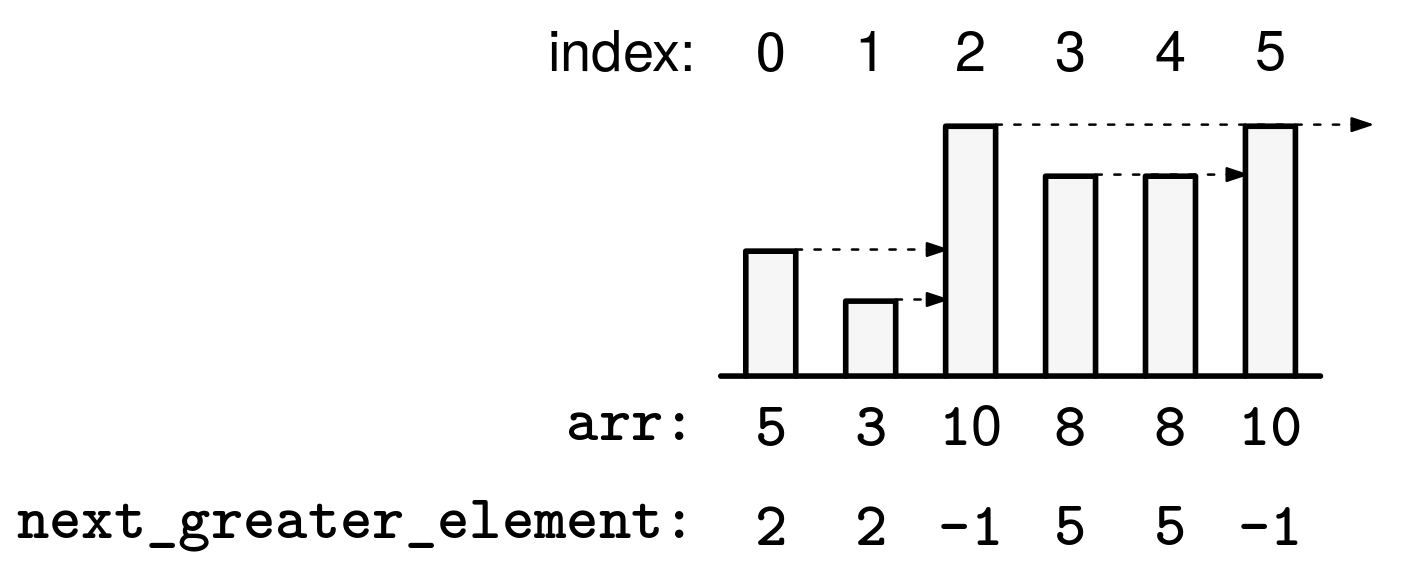
In Figure 2, NGE[i] is the index of the next element in arr after i greater than arr[i], or -1 if there is no greater element after it.
Solution 5: Next Greater Element
Full code & other languages →The naive solution starts at each index, scans forward to find the next greater element, and repeats that for each index. This takes O(n^2) time, where n is the size of the array. We'll see how to use a monotonic stack to do it in linear time.
The key is that it is easier to populate the NGE array from right to left. At each index i, from n-1 to 0, we keep track of all the elements to the right of i that are potential candidates to be the NGE of some index to the left of i. We can think of this geometrically: if we think of each element in the array as a bar in a plot, the candidates are all the elements "visible when looking to the right" from index i:
![When finding the NGE for arr[2], the candidates are visible elements to the right](/blog/monotonic-stacks-and-queues/fig3.png)
As we iterate right to left, we can track the NGE candidates in a stack, with candidates further right deeper in the stack. A small number to the right of a large number is not visible from the left side, so candidates will be ordered from smallest (top) to largest (bottom). In other words, the stack will be strictly monotonic decreasing, with the smallest candidate at the top. When we process each element arr[i], we discard any candidates smaller than or equal to arr[i], as they'll be behind arr[i] from this point onward. The first remaining candidate is the NGE of arr[i]. Or, if there are no candidates left, arr[i] has no NGE. Finally, arr[i] becomes a candidate for future iterations.
We can capture this logic in a recipe:
next_greater_element(arr)
initialize empty stack for NGE candidates
for each index i from right to left
pop all NGE candidates from the stack that are ≤ arr[i]
if the stack is not empty
the top of the stack is the NGE of i
else
index i has no NGE
add i to the stack
Recipe 1. Next greater element.
Here is the Python implementation:
def next_greater_element(arr):
n = len(arr)
nge = [-1] * n
stack = []
for i in range(n - 1, -1, -1):
while stack and arr[stack[-1]] <= arr[i]:
stack.pop()
if stack:
nge[i] = stack[-1]
stack.append(i)
return nge
Each element is pushed and popped from the stack at most once, so the time complexity is O(n).
Depending on the problem, we may need other variations, which can all be found with monotonic stacks:
index: 0 1 2 3 4 5
arr = [ 5, 3, 10, 8, 8, 10]
next_greater_element = [ 2, 2, -1, 5, 5, -1] (NGE)
next_smaller_element = [ 1, -1, 3, -1, -1, -1] (NSE)
prev_greater_element = [-1, 0, -1, 2, 2, -1] (PGE)
prev_smaller_element = [-1, -1, 1, 1, 1, 1] (PSE)
The other combinations can be computed by tweaking Recipe 1. We just need to flip the order of iteration and/or the comparison operator, so focus on learning NGE, and you'll be able to get the others too.
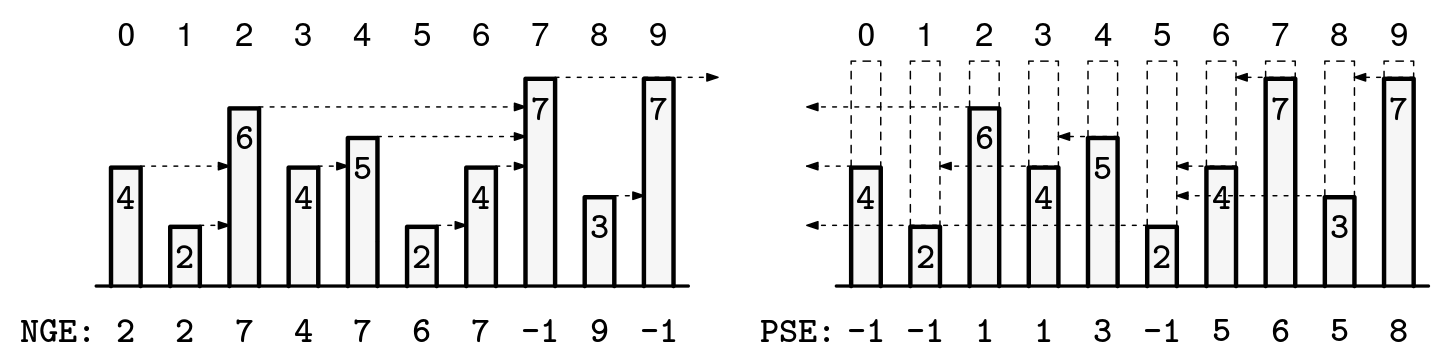
In array problems, it is sometimes useful to compute, for each index, the next (or previous) greater (or smaller) element. We can compute this for each index in linear time using monotonic stacks. To get NGE, NSE, PGE, and PSE, we just need to adjust the processing direction and the candidate comparison accordingly. We can even adjust the candidate comparison to find the next greater or equal element (rather than strictly greater). This applies to any variation.
NGE Applications
Computing the NGE array (or one of its cousins) in a preprocessing step can make some tricky array problems easier. For instance:
Problem 6: Largest Rectangle
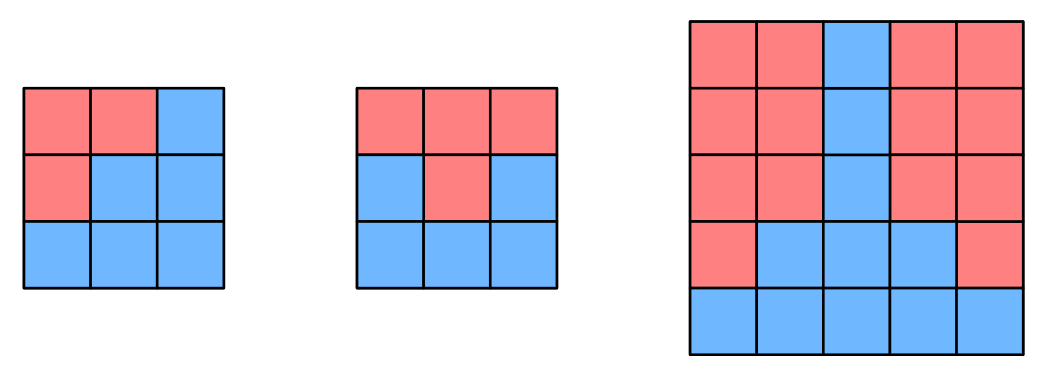
Try it yourself →You have an n×n mosaic made of blue and red tiles, where n > 0. You are given an array of integers, tiles, of length n, where tiles[i] indicates the number of blue tiles in column i of the mosaic (columns are 0-indexed). For each column, all the blue tiles are contiguously at the bottom, and the red tiles are contiguously at the top.
Return the size of the largest rectangle that can be formed using only blue tiles. The rectangle cannot contain partial tiles.
Example 1:
tiles = [1, 2, 3]
Output: 4
The mosaic is 3x3, and it looks like: The largest blue rectangle is 2x2 at the bottom right corner.
Example 2:
tiles = [2, 1, 2]
Output: 3
Example 3:
tiles = [1, 2, 5, 2, 1]
Output: 6
Solution 6: Largest Rectangle
Full code & other languages →One thing we can say for sure is that the base of the rectangle will be at the base of the mosaic. The problem is figuring out the other 3 boundaries.
The naive solution would be to consider all possible left and right boundaries (i.e., columns of the mosaic), 0 <= l <= r < n, and then look for the tallest blue rectangle that fits between those columns. The height of the tallest rectangle would be min(tiles[l:r+1]). The total runtime would be O(n3).
The property we need for this problem is: the top of the largest blue rectangle will touch at least one red tile (otherwise, we could make it taller and get a bigger one). That is, the height of the rectangle is tiles[i] for some i.
So, we can take each index i in tiles and ask, "What is the largest rectangle that includes column i and has height tiles[i]?
Per the property above, one of the rectangles found in this way must be the largest one.
So now let's focus on the question: "Given a fixed i, what is the largest rectangle that includes column i and has height tiles[i]?"
This question is easier because we have already fixed two of the boundaries: the base and the top. So we just need to know how far to the left and right we can extend the rectangle.
So, how far can we extend to the right? We can go up to the first column after i which has a height less than tiles[i].
The data structure that we need to answer this type of question is the "NSE" (Next Smaller Element) array. If NSE[i] = j, the right boundary is column j-1 (inclusive).
Similarly, to find the left boundary, we can use the "PSE" (Previous Smaller Element) array. If PSE[i] = j, the left boundary is column j+1 (inclusive).
So, for each i, the largest rectangle that includes column i and has height tiles[i] goes from PSE[i] + 1 (inclusive) to NSE[i] - 1 (inclusive) and has a width of NSE[i] - PSE[i] - 1. The area of this rectangle is (NSE[i] - PSE[i] - 1) * tiles[i].
We can compute the NSE and PSE arrays in O(n) time, and then use them to consider all columns in O(n) time. The total runtime is O(n).
To compute the NSE and PSE arrays, we adapt Recipe 1. We just modify the comparison operator and the direction of the traversal appropriately (see the full implementation online).
def largest_rectangle(tiles):
n = len(tiles)
nse = next_smaller_element(tiles)
pse = prev_smaller_element(tiles)
max_area = 0
for i in range(n):
width = nse[i] - pse[i] - 1
area = width * tiles[i]
max_area = max(max_area, area)
return max_area
NGE Problem Set
Try to use Recipe 1 to solve the following problems:
Problem 7: King Kong Vs Godzilla
Try it yourself →King Kong and Godzilla are rampaging a city. You're given a non-empty array of positive integers, street, representing the heights of buildings in a street from left to right.
- King Kong starts at the beginning of the street and prefers to smash tall buildings. King Kong will only spare a building
street[i]if there is a taller building to the right. - Godzilla starts at the end of the street and prefers crushing small buildings. Godzilla will only spare a building
street[i]if there is a shorter building to the left.
Return a boolean array of length n, where n is the length of street, indicating which buildings were spared by both King Kong and Godzilla. Index i should be true if street[i] was spared.
Example 1:
street = [10, 20, 30, 15, 5]
Output: [False, True, False, False, False]
King Kong spares 10 and 20 because a taller building is to the right of each of those.
Godzilla spares 15, 30, and 20 because a shorter building is to the left of each of those.
The only building spared by both is 20.
Example 2:
street = [10, 20, 30, 40, 50]
Output: [False, True, True, True, False]
King Kong destroys the last building, and Godzilla destroys the first one.
Example 3:
street = [50, 40, 30, 20, 10]
Output: [False, False, False, False, False]
King Kong destroys all buildings, and so does Godzilla.
Example 4:
street = [1, 10, 5, 20]
Output: [False, True, True, False]
Solution 7: King Kong Vs Godzilla
Full code & other languages →This is the type of problem where it makes sense to immediately decrease the difficulty. We can tackle the easier problem where there is only King Kong. It will help us avoid mixing up left/right and taller/shorter, which can easily throw us off.
Buildings spared by King Kong
We can express if building i is spared by King Kong in two ways, which are equivalent but lead to different approaches:
street[i] >= max(street[i + 1:n]).street[i]has no next greater element.
The first approach leads to a "suffix max" type of approach, while the second is based on the 'next greater element' technique.
Suffix max approach for King Kong
The naive solution is to iterate over each suffix and find the maximum. This takes O(n^2) time. We can do better with a MaxQueue data structure (Problem 1).
If we implement this data structure, we can push all the buildings to it, and then, for each index i from left to right, remove it. The maximum value in the queue will be the maximum building height to the left of building i.
def spared_by_king_kong(street):
n = len(street)
spared = [False] * n
# Add all buildings to the queue (except the first one)
max_queue = MaxQueue()
for i in range(1, n):
max_queue.push(street[i])
# Process each building (except the last one, which is always destroyed)
for i in range(n - 1):
if street[i] < max_queue.max():
spared[i] = True
max_queue.pop()
return spared
NGE approach for King Kong
The next greater element approach is based on the observation that a building is spared by King Kong if it has no next greater element.
We can use Recipe 1 to compute the NGE array for street in O(n) time. Importantly for us, we can set NGE[i] = -1 for elements that have no next greater element. It's then straightforward to iterate over street and check if NGE[i] == -1. If it is, then building i is not spared by King Kong.
def spared_by_king_kong(street):
n = len(street)
# Build NGE array using Recipe 1.
nge = [-1] * n
stack = []
for i in range(n - 1, -1, -1):
while stack and street[stack[-1]] <= street[i]:
stack.pop()
if stack:
nge[i] = stack[-1]
stack.append(i)
# Building i is spared if it has a next greater element.
spared = [False] * n
for i in range(n):
if nge[i] != -1:
spared[i] = True
return spared
Buildings spared by Godzilla
Now that we handled King Kong, we can turn our attention to Godzilla. We could adapt our King Kong approach:
- If we followed the
MaxQueueapproach, we could reverse the direction of iteration and use aMinQueueinstead of aMaxQueue. - If we followed the
NGEapproach, we could compute thePSE(previous smaller element) instead.
However, there is a trick we can use to reuse the King Kong solution with a bit of preprocessing and postprocessing:
- We can reverse the
streetarray to simulate Godzilla's view. - We can negate the height values so that shorter buildings appear taller and vice versa.
- We can then run King Kong's algorithm on the reversed and negated array.
- Don't forget to reverse the result array to get the final answer.
For example, [10, 20, 30, 15, 5] becomes [-5, -15, -30, -20, -10]. Since negative numbers can be confusing, let's add 30 to every element to make it easier to understand: [25, 15, 0, 10, 20] (this doesn't change the relative 'heights'). Given this array, King Kong would smash 25 and 15 and 20 and output:
spared = [False, False, True, True, False].
Reversing that, we get that Godzilla would spare:
[False, True, True, False, False].
def spared_by_godzilla(street):
new_street = [-h for h in street]
new_street.reverse()
res = spared_by_king_kong(new_street)
res.reverse()
return res
Complete solution
Finally, we can combine the two solutions to get the final answer:
def spared(street):
res1 = spared_by_king_kong(street)
res2 = spared_by_godzilla(street)
return [a and b for a, b in zip(res1, res2)]
Analysis
Each MaxQueue operation takes amortized constant time, so the overall time complexity for the first approach is O(n). Computing the NGE array takes O(n) time, so the overall time complexity for the second approach is also O(n).
Problem 8: King Kong Vs Godzilla In The Fog
Try it yourself →King Kong and Godzilla are (still) rampaging a city. You're given a non-empty array of positive integers, street, representing the heights of buildings in a street from left to right. It is foggy, so King Kong and Godzilla can only see the next k buildings in front of them.
- King Kong starts at the beginning of the street and prefers to smash tall buildings. King Kong will only spare a building
street[i]if there is a taller building to the right less thankbuildings away. - Godzilla starts at the end of the street and prefers crushing small buildings. Godzilla will only spare a building
street[i]if there is a shorter building to the left less thankbuildings away.
Return a boolean array of length n, where n is the length of street, indicating which buildings were spared by both King Kong and Godzilla. Index i should be true if street[i] was spared.
Example 1:
street = [10, 20, 30, 15, 5], k = 2
Output: [False, True, False, False, False]
King Kong does the following:
1. King Kong starts at building 10 and can see the next 2 buildings: 20 and 30.
It spares it since it sees a taller building (20).
2. King Kong moves to building 20 and can see the next 2 buildings: 30 and 15.
It spares 20 since it sees a taller building (30).
3. King Kong moves to building 30. It can see the next 2 buildings: 15 and 5.
It destroys 30 since it is taller than the other buildings it sees.
4. King Kong moves to building 15. It can see the next building: 5.
It destroys 15 since it is taller than the other buildings it sees.
5. King Kong moves to building 5. There are no more buildings to see.
It destroys 5 since it is the last building.
Godzilla does the following:
1. Godzilla starts at building 5 and can see the next 2 buildings: 15 and 30.
It destroys 5 since it sees a taller building (15).
2. Godzilla moves to building 15 and can see the next 2 buildings: 30 and 20.
It destroys 15 since it sees a taller building (30).
3. Godzilla moves to building 30. It can see the next 2 buildings: 20 and 10.
It spares 30 since it sees a shorter building (20).
4. Godzilla moves to building 20. It can see the next building: 10.
It spares 20 since it sees a shorter building (10).
5. Godzilla moves to building 10. There are no more buildings to see.
It destroys 10 since it is the last building.
The only building spared by both is 20.
Example 2:
street = [1, 10, 5, 20], k = 2
Output: [False, True, True, False]
Example 3:
street = [1, 10, 5, 20], k = 1
Output: [False, False, False, False]
Building (10) has a taller building (20) to the right, but it is hidden by the fog.
Solution 8: King Kong Vs Godzilla In The Fog
Full code & other languages →As in Problem 7, this is the type of problem where it makes sense to immediately decrease the difficulty. We will focus on the easier problem where there is only King Kong. We can handle Godzilla in an analogous way to Solution 7 (you can find the full solution online).
We can express if building i is spared by King Kong in two ways, which are equivalent but lead to different implementations:
street[i] >= max(street[i + 1:i + k + 1])next_greater_element(i) > i + k
The first approach leads to a sliding window approach with a MaxQueue, while the second is based on the 'next greater element' technique.
We'll show the second approach (the first one is online).
We can use Recipe 1 to compute the NGE array for street in O(n) time. This array has the same length as street and NGE[i] is the index of the next greater element of street[i], or -1 if there is none:
It's then straightforward to iterate over street and check, for each building, if the NGE exists and is within the next k buildings. If so, the building is spared by King Kong.
def spared_by_king_kong(street, k):
n = len(street)
# Build NGE array using Recipe 1.
nge = [-1] * n
stack = []
for i in range(n - 1, -1, -1):
while stack and street[stack[-1]] <= street[i]:
stack.pop()
if stack:
nge[i] = stack[-1]
stack.append(i)
# Building i is spared if NGE[i] exists and is within k buildings.
spared = [False] * n
for i in range(n):
if nge[i] != -1 and nge[i] <= i + k:
spared[i] = True
return spared
Key Takeaways
We touched on two advanced applications of stacks and queues, monotonic stacks and queues (double-ended queues, to be precise), which have two killer applications:
Monotonic deques: 'max queue' and sliding maximums.
Monotonic stacks: next greater element (Recipe 1).
If we learn to implement max queues (Solution 1) and compute the NGE array (Recipe 1) on the spot, we can add these techniques to our toolkit for dealing with tough array-based problems. The nice part is that we can compute them in a preprocessing step, so the implementation doesn't change from problem to problem. We should only implement once we know how we'll use them.
Footnotes
-
For JS, to get running code, we need to provide a deque implementation (or use a third-party one). ↩