Counting Islands in a Grid: DFS or BFS?

Which algorithm is better for the Count Islands in a Grid problem, DFS or BFS?
In this classic LeetCode problem, we have a grid where 0's represent water and 1's represent land, and we need to count the number of islands (connected components) present. Try it yourself!
So, should we use DFS or BFS? Counting connected components is a basic graph problem, so you'd think there is not much to it.
It's more contentious than you'd think.
In this post, we'll use the different strengths of DFS and BFS to push the space complexity from O(R*C) to O(1).
Naive solution
Since we don't care about distances, any graph traversal will do: both DFS and BFS solve the problem in linear time and linear extra space.
For instance, here is a BFS solution:1
directions = [(-1, 0), (1, 0), (0, 1), (0, -1)]
# Returns if (r, c) is in bounds, "walkable", and not visited.
def is_valid(r, c, grid, visited):
R, C = len(grid), len(grid[0])
return 0 <= r < R and 0 <= c < C and grid[r][c] == 1 and (r, c) not in visited
def grid_bfs(start_r, start_c, grid, visited):
queue = deque([(start_r, start_c)])
while queue:
r, c = queue.popleft()
for dir_r, dir_c in directions:
nbr_r, nbr_c = r + dir_r, c + dir_c
if is_valid(nbr_r, nbr_c, grid, visited):
visited.add((nbr_r, nbr_c))
queue.append((nbr_r, nbr_c))
def count_islands(grid):
R, C = len(grid), len(grid[0])
island_count = 0
visited = set()
for r in range(R):
for c in range(C):
if is_valid(r, c, grid, visited):
visited.add((r, c))
grid_bfs(r, c, grid, visited)
island_count += 1
return island_count
Trick: modifying the input grid
Linear time for this problem is already optimal. Where it gets interesting is if we are allow modifying the input grid to save extra space.
Instead of tracking visited cells in a separate data structure, we can use a special value, like 2, directly in the input grid.
Then, the extra space is based on:
- The recursion stack for DFS
- The queue for BFS
With this optimization, suddenly BFS is better than DFS.
Why?
On the one hand, DFS is recursive, and the call stack still counts as extra space. In the worst case, we could zig-zag through the entire grid with DFS, making O(R * C) nested calls.2
On the other hand, BFS explores the nodes layer by layer, sorted by distance (first the nodes at distance 1, then the nodes at distance 2, and so on). BFS includes nodes from at most two distance layers in the queue at any given time.
Here is the optimized BFS solution:
directions = [(-1, 0), (1, 0), (0, 1), (0, -1)]
# Returns if (r, c) is in bounds, "walkable", and not visited (indicated by 2).
def is_valid(r, c, grid):
R, C = len(grid), len(grid[0])
return 0 <= r < R and 0 <= c < C and grid[r][c] == 1
def grid_bfs(start_r, start_c, grid):
queue = deque([(start_r, start_c)])
while queue:
r, c = queue.popleft()
for dir_r, dir_c in directions:
nbr_r, nbr_c = r + dir_r, c + dir_c
if is_valid(nbr_r, nbr_c, grid):
grid[nbr_r][nbr_c] = 2
queue.append((nbr_r, nbr_c))
def count_islands(grid):
R, C = len(grid), len(grid[0])
island_count = 0
for r in range(R):
for c in range(C):
if is_valid(r, c, grid):
grid[r][c] = 2
grid_bfs(r, c, grid)
island_count += 1
return island_count
BFS extra space analysis
Surprisingly, analyzing the extra space complexity of BFS is the hardest part of this problem.
Let's define count(R, C) as the maximum size of a "distance layer": the number of cells in an RxC binary grid (where 0's act as 'water') that can be equidistant from a given cell.
The extra space of BFS is O(count(R, C)) because the BFS queue only contains cells from at most two distance layers at once, so len(queue) <= 2 * count(R, C).
So, what is count(R, C)?
Let's tackle this question, starting with an easier case:
In a grid without any 'water', each distance layer forms a diamond shape, which contains at most two nodes in any given row or column:

Thus, count(R, C) <= min(2*R, 2*C) = O(min(R, C)).
However, if we allow 'water' (0's) in the grid, it is no longer true that there are at most two nodes in any given row or column at the same distance from the starting node:
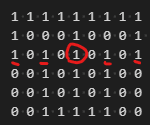
The grid above has four 1's in the same row at distance 8 from the circled 1.
Astonishingly, it turns out that the BFS queue may grow to Θ(min(R, C)^2) in the worst case.
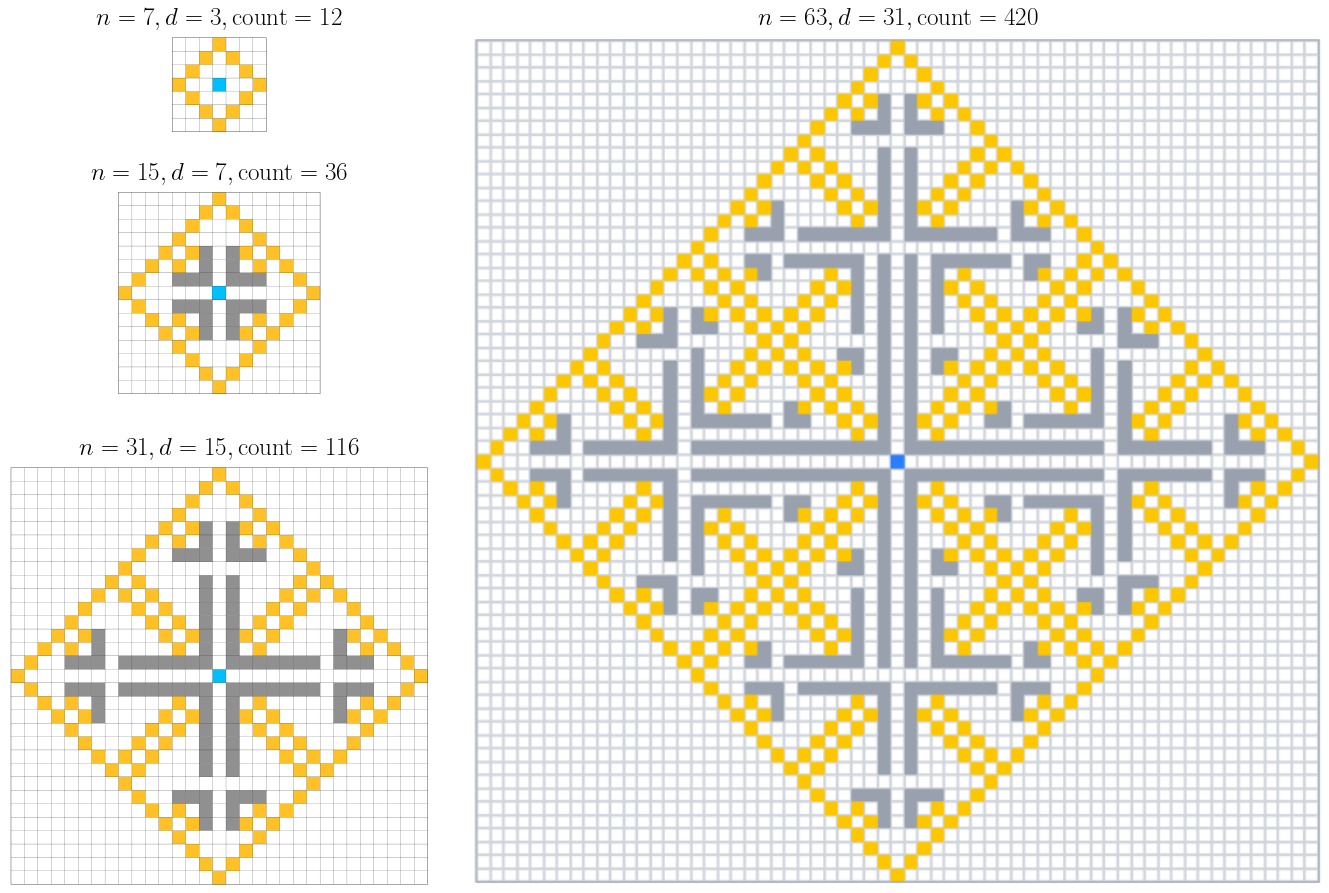
To show this, we need to construct a very specific grid arrangement that maximizes the number of cells equidistant from the starting cell. The construction follows a recursive pattern.3
Here is the recursive construction for a 127x127 grid, which has 1588 cells (in yellow) at distance 63 from the starting cell (in blue).
- Gray cells are 0's (the 'water')
- Every other cell is a 1 (blue, yellow, and white)

All the yellow cells will be in the BFS queue at the same time.
The construction works for square grids where the side n is a power of 2 minus 1:
The following diagram illustrates the general case of the recursive construction:
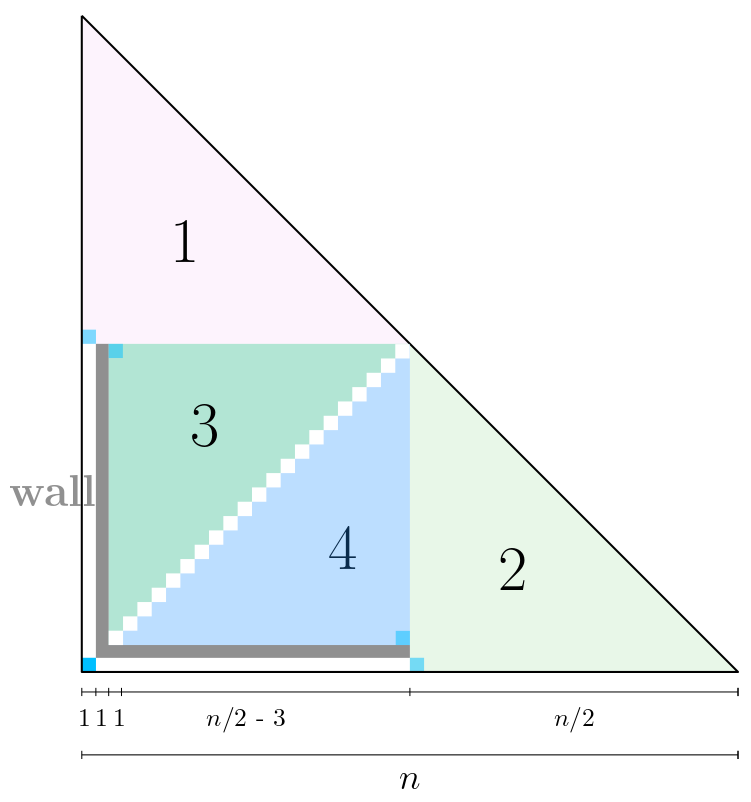
We can see how an 'L' shaped water wall allows us to split one corner of the grid into four smaller corners.
- Subcorners 1 and 2, start at distance
n/2from the starting cell, and have dimensionsn/2 x n/2. - Subcorners 3 and 4, start at distance
n/2 - 3from the starting cell, and have dimensions(n/2 - 3) x (n/2 - 3).
Let count(n) be the maximum number of cells at distance n-1 from the corner of a grid triangle with side length n.
Our recursive construction says:
count(n) = 2 * count(n/2) + 2 * count(n/2 - 3)
Asymptotically, this is going to be equivalent to:
count(n) = 4 * count(n/2)
We also need a base case, of course, but since we are only interested in the asymptotic analysis, it suffices to say that count(n) is constant for values of n below some constant.
Asymptotically, this recurrence simplifies to count(n) = Θ(n^2).
This is because the recurrence tree has log_2(n) levels, and at each level the number of terms is multiplied by 4, so the total number of terms is roughly 4^log_2(n).
Now, doing a bit of logarithm arithmetic, we get:
4^log_2(n) = (2^2)^log_2(n) = 2^(2*log_2(n)) = 2^(log_2(n^2)) = n^2
We can now compare the extra space complexity of DFS and BFS in the worst case. DFS uses O(R*C) extra space (as exemplified by a zig-zag pattern over a grid with all 1's) while BFS uses O(n^2) (as exemplified by this recursive pattern).
BFS is a slight improvement over DFS in two ways:
- If the grid is thin or tall (many more rows than columns or vice versa),
O(min(R, C)^2)is better thanO(R*C). - The worst-case for BFS is a lot more contrived, so BFS will use less space on average or on expectation.
Iterative DFS
But this is not the end of the journey.
We can push the extra space down all the way to O(1), but we have to switch back to DFS!
With O(1) extra space, we can't afford recursion at all, so we have to use iterative DFS.
Iterative DFS typically uses an explicit stack; however, we can utilize the input grid itself to track the index of each cell in the DFS stack. Since the input already uses values 0 and 1, we can use negative numbers to track the stack: -1 for the first cell in the stack, -2 for the second, and so on.
The reason why we can't bring BFS down to O(1) extra space is that when BFS explores the grid, it jumps around all over the place. Without storing pending nodes in an explicit queue, we don't know where to go next. DFS is our friend because it always explores from the same "head" of the path, which we can easily track with just a couple of extra variables (head_row, head_col).
Here is the iterative DFS solution:
directions = [(-1, 0), (1, 0), (0, 1), (0, -1)]
def in_bounds(r, c, grid):
R, C = len(grid), len(grid[0])
return 0 <= r < R and 0 <= c < C
# Finds the parent in the stack (neighbor with less negative stack value by 1)
def find_parent(r, c, grid):
current_value = grid[r][c]
for dr, dc in directions:
nbr_r, nbr_c = r + dr, c + dc
if in_bounds(nbr_r, nbr_c, grid) and grid[nbr_r][nbr_c] == current_value + 1:
return nbr_r, nbr_c
return None, None
def find_unvisited_neighbor(r, c, grid):
for dr, dc in directions:
nbr_r, nbr_c = r + dr, c + dc
if in_bounds(nbr_r, nbr_c, grid) and grid[nbr_r][nbr_c] == 1:
return nbr_r, nbr_c
return None, None
def iterative_dfs(start_r, start_c, grid):
stack_level = -1
grid[start_r][start_c] = stack_level
head_r, head_c = start_r, start_c
while stack_level < 0:
nbr_r, nbr_c = find_unvisited_neighbor(head_r, head_c, grid)
if nbr_r is not None:
stack_level -= 1
grid[nbr_r][nbr_c] = stack_level
head_r, head_c = nbr_r, nbr_c
else:
# No unvisited neighbors, backtrack
stack_level += 1
head_r, head_c = find_parent(head_r, head_c, grid)
def count_islands(grid):
R, C = len(grid), len(grid[0])
island_count = 0
for start_r in range(R):
for start_c in range(C):
if grid[start_r][start_c] == 1:
iterative_dfs(start_r, start_c, grid)
island_count += 1
return island_count
Final thoughts
I found it cool how, with more optimizations, we went from "both are the same" to "BFS is better" to "DFS is better". Thanks to a BCtCI reader for suggesting the BFS + grid modification combination.
Want to leave a comment? You can post under the linkedin post or the X post.
Footnotes
-
LeetCode uses strings for the cell values, but we use integers for simplicity. ↩
-
This is also the reason why, for DFS, we need to worry about stack overflow for large grids. ↩
-
Credit to Timothy Johnson for this idea. ↩