Get Binary Search Right Every Time, Explained Without Code

One of the things that makes binary search tricky to implement is that you usually need to tweak the pointer manipulation logic in subtle ways based on the specifics of the problem.

E.g., an implementation that works for finding a target in a sorted array when the target is present, may not work if the target is missing. Or, it may not be clear how to tweak the code to find the last occurrence of the target instead of the first one. And of course, there are plenty of less conventional applications of binary search where the input is not an array, like catching bike thieves.

In Beyond Cracking the Coding Interview, we wanted to simplify this, so we went looking for a general binary search template. Going into it, I thought we might need at least two templates, but we ended up with just one, which we called the "transition point recipe", and which works for every problem we tried, including the 17 problems in the binary search chapter of the book. If you find one where it doesn't work, let me know!

The transition point problem

Here is the thesis of the transition point recipe:

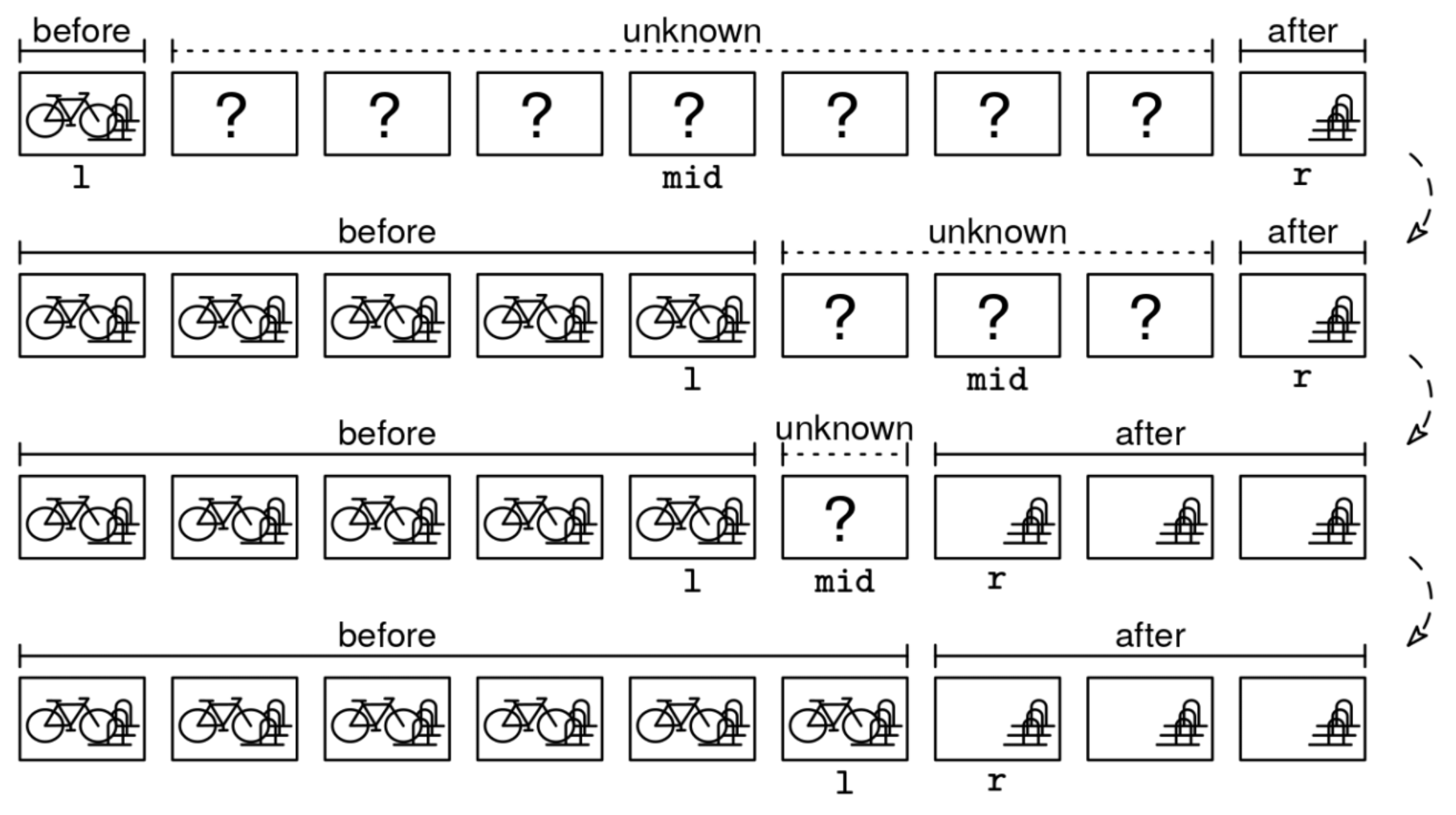
In the 'transition point problem', you are given an array with just two values, say 1 and 2, where all the 1s come before the 2s, and you need to point where it changes.

E.g., in the array [1, 1, 1, 1, 1, 2, 2, 2], the last 1 is at index 4 and the first 2 is at index 5.

Knowing how to solve this specific problem is key to our recipe. The specific binary search implementation is not important, but there is an invariant we can follow that makes it quite easy: ensure that the left pointer is always at a 1 and the right pointer is always at a 2.

We give code in the book, but remembering exact code in an interview is error prone. Instead, the four bullet points below are all I personally remember, and I feel confident that I can derive the rest easily.

1. Start by handling some edge cases:
   • The array is empty
   • Every value is 1
   • Every value is 2
2. Initialize two pointers, left and right, to the first and last indices, respectively.
3. For the main binary search loop, always maintain the invariant that the value at left is 1 and the value at right is 2. Let this invariant guide your pointer manipulation logic, so that you don't need to memorize any code.
4. Stop when the left and right pointers are next to each other (i.e., left + 1 == right).

Combining the invariant with the stopping condition, we get that, at the end, left will be at the last 1 and right will be at the first 2.

These bullet points rely on two ideas to make binary search easier: (1) handling edge cases upfront, and (2) letting strong invariants guide the implementation. Notice how the invariant even guides the edge cases at the beginning, as they are the necessary ones to be able to initialize left and right in a way that satisfies it.

The reduction

Ok, so now, let's take for granted that we can solve the transition point problem. How does this help us solve other binary search problems?

The idea is to come up with a (problem-specific) predicate, like < target, >= target, or x % 2 == 0, which splits the search range into two regions, the "before" region and the "after" region.

This predicate is a function that takes an element of the search range and returns a boolean, and -- as you probably saw coming -- it is key that the all the elements with true values come before the elements with false values (or the other way around).

Then, we can use the solution to the transition point problem to find the transition point between the 'before' and 'after' regions. The only difference is that, instead of checking boolean values directly, we check the result of the predicate.

You can even wrap the predicate in a function, which we called is_before(x) in the book, which tells you whether a given element is in the 'before' region. Then, it's really obvious that we are just solving the transition point problem every time.

The only part that requires some thinking is choosing the right transition point. For example:

• if we want to find the first occurrence of target in a sorted array, we can use is_before(x) = x < target, which means that, if target is present, the first occurrence is the first element in the 'after' region (so, we can check/return the right pointer at the end).
• if we want to find the last occurrence of target in a sorted array, we can use is_before(x) = x <= target, which means that, if target is present, the last occurrence is the last element in the 'before' region (so, we can check/return the left pointer at the end).

And so on for other problems.

Practice

You can try the transition-point recipe on all the problems from the binary search chapter of the book online at start.interviewing.io/beyond-ctci/part-vii-catalog/binary-search, even if you don't have the book. There, you can also find all our solutions using the recipe, in Python, JS, Java, and C++.

By the way, the binary search chapter of the book is free -- it's in bctci.co/free-chapters.

Want to leave a comment? You can post under the linkedin post or the X post.